стандартная задача на комбинаторику
1*2*2*3*2*4*2*4*3=2304
эти числа это количества делителей у чисел 1 2 ... 9
У числа 6 есть делить 2(для ответа сверху)
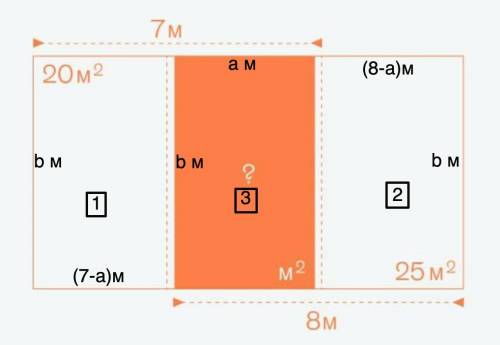
Площадь маленького прямоугольника внутри большого прямоугольника равна 15 м².
Пошаговое объяснение:
Надо найти площадь маленького (оранжевого) прямоугольника внутри большого.
Вспомним формулу площади прямоугольника:
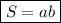, где а и b - ширина и высота прямоугольника.
Обозначим ширину искомого прямоугольника №3 - а м, высоту - b м
⇒ 
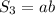
Тогда ширина прямоугольника №1 - (7-а) м,
а прямоугольника №2 - (8-а) м.
Высоты этих прямоугольников равны - b м.
А площади этих прямоугольников будут соответственно равны:
Для того, чтобы найти искомую площадь, надо найти ширину и высоту прямоугольника №3.
1. Выразим b из площади прямоугольника №1:
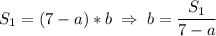
Подставим значение площади S₁ = 20 м² в полученное выражение:
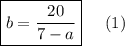
2. Выразим b из площади прямоугольника №2:
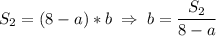
Подставим значение площади S₂ = 25 м² в полученное выражение:
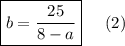
3. Приравняем выражения (1) и (2) и найдем а.
Воспользуемся основным свойством пропорции:
Произведение крайних членов равно произведению средних членов.
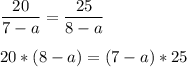
Раскроем скобки. Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный и решим уравнение:
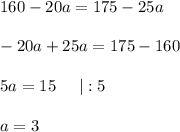
⇒ ширина маленького прямоугольника равна 3 м.
4. Подставим значение а=3 в (1) или (2) равенства и найдем b.
Подставим в (1):
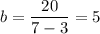
⇒ высота маленького прямоугольника равна 5 м.
5. Теперь, зная ширину и высоту, можем найти площадь маленького прямоугольника №3:
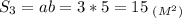
⇒ Площадь маленького прямоугольника равна 15 м².
ответ: Задача 1. Случайная величина X задана дифференциальной функцией распределения
1) Определить вероятность попадания случайной величины X в интервал [π,5/4π]
[
π
,
5
/
4
π
]
.
2) Найти математическое ожидание и дисперсию случайной величины X.
Посмотреть решение
Задача 2. Случайная величина X задана плотностью вероятности:
Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α < X < β);
д) построить графики f(x) и F(x).
Посмотреть решение
Задача 3. Случайная величина Х задана функцией распределения F(x).
А) является ли случайная величина Х непрерывной?
Б) имеет ли случайная величина Х плотность вероятности f(X)? Если имеет, найти ее.
В) постройте схематично графики f(X) и F(X).
Решение: равномерное распределение
Задача 4. Дана функция распределения F(x) непрерывной случайной величины X.
1. Найти значения параметров a,b
2. Построить график функции распределения F(x)
3. Найти вероятность P(α < X < β)
4. Найти плотность распределения p(x) и построить ее график.
Пример решения: экспоненциальный закон
Задача 5. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: f(t)=2e-2t при t ≥ 0 и f(t)=0 при t<0.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.
Решение: показательный закон
Задача 6. Функция распределения вероятностей случайной величины X
X
имеет вид:
А) найти a
a
и b
b
;
Б) найти плотность f(x)
f
(
x
)
;
В) нарисовать график F(x)
F
(
x
)
;
Г) нарисовать график f(x)
f
(
x
)
;
Д) найти M[X]
M
[
X
]
;
Е) найти D[X]
D
[
X
]
.
Пошаговое объяснение:
посчитаем сколько таких чисел может быть:
для 1ой цифры вариант только один: 1
для 2ой цифры вариантов 2: 1 и 2
для 3ей цифры вариантов 2: 1 и 3
для 4ой цифры вариантов 3: 1,2,4
для 5ой цифры вариантов 2: 1 и 5
для 6той цифры вариантов 3: 1,3,6
для 7ой цифры вариантов 2: 1 и 7
для 8ой цифры вариантов 4: 1,2,4,8
для 9ой цифры вариантов 3: 1,3,9
узнаём полное количество вариантов ,перемножим:
1*2*2*3*2*3*2*4*3 = 1728
ответ: 1728!