см рисунок!
находим длинну диагонали:
AC=корень квадратный (AM^{2}+AC^{2}) (по теореме пифагора)
AM=AD-MD
MD=(AD-BC)/2=(21-11)/2=5
AM=21-5=16
CM=корень квадратный (CD^2-MD^2)=корень квадратный (13^2+5^2)=12
AC=корень квадратный (16^2+12^2)=20
высота призмы ровна часному от деления площади сечения призмы на длинну диагонали:
H=180/20=9
Площадь поверхности ризмы равна сумме площадей боковых поверхностей и площадей оснований
S=S1+2*S2
S1 равна произведению периметра трапеции на высоту призмы
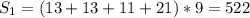
S2 равна площади трапеии
S2=((BC+AD)/2)*H=((21+11)/2)*12=192
S=192*2+522=906
Число делится на 2, если оканчивается на 0, либо арследняя его цифра делится на 2, то есть, все четные числа делятся на 2.
Число делится на 4, если оканчивается на 00 или, две его последние цифры образуют число, кратное 4 (делящееся на 4 без остатка).
а) Если число делится на 4, то оно обязательно делится и на 2, потому, что в признаки делимости на 2, входят в признаки делимости на 4: числа, кратные 4 - всегда четные; если число заканчивается на 00, то последняя его цифра - 0, а это - признак делимости на 2.
б) Если число делится на 2, то нельзя утверждать, что оно, также. делится на 4, потому, что, если не будет соблюдено условие кратности 4-м, числа, составленного из последних цифр, либо число будет оканчиваться на 1, 3, 5 или более, нулей, то оно будет делиться на 2, будет четным, но на 4 делиться не будет.
Пример:
5848 - четное, последняя цифра делится на 2 (8/2), число, составленное из 2-х последних цифр, кратно 4 (48/4=12).
Вывод: число 5848 делится на 2, и на 4.
5840 - четное, оканчивается на 0, число, составленное из 2-х последних цифр кратно 4.
Вывод: число делится на 2. и на 4.
5842 - четное, последняя цифра делится на 2, число, составленное из 2-х последних цифр не кратно 4 (42/4=10.5)
Выпод: делится на 2, но не делится на 4.
1. нАЙТИ ДЛИНУ ДИАГОНАЛИ ОСНОВАНИЯ.
Обозначим его ABCD, AB - короткое снование, CD - длинное основание.
Опустим перпендикуляр из A на основание CD, он отсечет на нем отрезок CK 5 см. Получится прямоугольный треугольник ACK с гипотенузой 13 см и катетом 5 см. По теореме Пифагора: корень из (13 в квадрате-5 в квадрате)=12 см.
Теперь в треугольнике AKD ищем гипотенузу тоже по теореме Пифагора: корень из (12 в квадрате+16 в квадрате)=20 см.
Значит высота призмы равна 180/20=9 см.
2. Теперь вычисляем площадь поверхности:
площадь основания: половина суммы оснований трапеции на ее высоту: (11+21)/2*12=192, их у нас 2
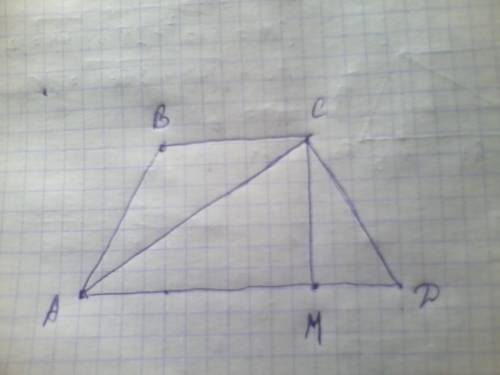
площадь боковой поверхности: периметр основания на высоту: (11+21+13+13)*9=522
Итого: 192*2+522=906 см в квадрате