Положим так. Если А1 танцевал с Б1, а А2 танцевал с Б2, то А1 танцевал с Б2, а А2 танцевал с Б1. Есть какое-то множество девочек М1, с которыми танцевал мальчик А1; и множество девочек М2, с которыми танцевал мальчик Б2. Оба множества непусты ввиду первых двух предложений.
Гипотеза указывает, что мальчик А1 танцевал с любой девочкой из М2. Множество М1 можно пополнять до тех пор, пока остаются другие нерассмотренные мальчики помимо А1; и если множество М1 ещё не включает всех девочек, то, ввиду предложения о наличии затанцованного мальчика для каждой девочки, такие мальчики остаются. Значит, А1 танцевал со всеми девочками, противоречие.
ответ: (-1;1)
Пошаговое объяснение:
5k - 3,6 _> 2(4k - 2,4) + 0,2
5k - 3,6 ≥ 8k - 4,8 + 0,2
5k - 8k ≥ - 4,8 + 0,2 +3,6
- 3k ≥ -1
k ≤ - 1:( - 3 )
k ≤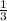
Наибольшее целое решение этого неравенства число 0 . Оно входит в промежуток (-1;1).
ответ А.