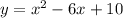
y = x ^ 2 + 6x + 10 Xc = -b / 2a = -6/2 = -3 yc = ( -3 ) ^ 2 + 6 ( -3 ) + 10 = 9 - 18 + 10 = 19 - 18 = 1 Вершина в точке ( -3 ; 1 )
Пошаговое объяснение:
(-2 1/6 - 3 1/4) : 2 3/5 + 2/3 * 2 1/4 - 5 1/6 = - 5 3/4
1) - 2 1/6 - 3 1/4 = - (2 2/12 + 3 3/12) = - 5 5/12
2) - 5 5/12 : 2 3/5 = - 65/12 : 13/5 = - 65/12 * 5/13 = - (5*5)/(12*1) = - 25/12 = - 2 1/12
3) 2/3 * 2 1/4 = 2/3 * 9/4 = (1*3)/(1*2) = 3/2 = 1 1/2
4) - 2 1/12 + 1 1/2 = - 2 1/12 + 1 6/12 = - (1 13/12 - 1 6/12) = - 7/12
5) - 7/12 - 5 1/6 = - (7/12 + 5 2/12) = - 5 9/12 = - 5 3/4
Пояснения:
1/6 = (1*2)/(6*2) = 2/12 - доп.множ.2
1/4 = (1*3)/(4*3) = 3/12 - доп.множ.3
5 5/12 = (5*12+5)/12 = 65/12
2 3/5 = (2*5+3)/5 = 13/5
2 1/4 = (2*4+1)/4 = 9/4
2 1/12 = 1 13/12
9/12 = (9:3)/(12:3) = 3/4 - сократили на 3
Пошаговое объяснение:
1 . a) (x⁵+1)dy = dx - диф. рівняння з відокремлюваними змінними :
dy = dx/( x⁵+1) - інтегруємо ;
∫ dy = ∫ dx/( x⁵+1) ;
у = ∫ dx/( x⁵+1) - це табличний інтеграл , який треба взяти з будь-якого
онлайн- калькулятора , тоді буде готово .
б) 2y" + y' - 5y = 0 ; записуємо його характеристичне рівняння :
2k² + k - 5 = 0 ; D = 1 + 40 = 41 > 0 ; k₁,₂ = ( - 1 ± √41 )/4 ;
y = C₁ e^( ( - 1 - √41 )/4 )x + C₂ e^( ( - 1 + √41 )/4 )x - загальний розв"язок .
в) y" - 3y' + 10y = 0 ; y( 0 ) = 1 , y '( 0 ) = 0 ;
k² - 3k + 10 = 0 ; D = - 31 < 0 ; k₁,₂ = ( 3 ± i √31)/2 ;
У заг = e^(3/2 x)( C₁cos√31/2 x + C₂sin √31/2 x ) ;
y( 0) = 1 = e⁰( C₁cos0 + C₂sin0) ; C₁ = 1 ;
y '( x ) = 3/2 e^( 3/2 x)( cos√31/2 x + sin√31/2 x) + e^(3/2 x)( - sin√31/2 x +
+ C₂cos√31/2 x) ;
y '(0) = 3/2 e⁰( cos0 + C₂sin0) + e⁰ (- sin0 + C₂cos0) = 0 ;
3/2 * 1 + 1 * C₂ = 0 ; C₂ = - 3/2 = - 1,5 ;
отже , У част = e^( 3/2 x)(cos√31/2 x - 1,5sin√31/2 x ) - це відповідь .
ответ:100% правильно
Пошаговое объяснение:
x=-8/2=-4
y=16-24+12=4 (-4; 4)