Проведем прямую через точку C параллельно DG; пусть она пересекает отрезок AD в точке F. Применим теорему о пропорциональных отрезках к углу BAG, стороны которого пересекают параллельные прямые DG и FC:
DF:FA=GC:CA; DF:FA=4:1. То есть точка F делит отрезок DA на отрезки, один из которых в 4 раза длиннее другого. Чтобы найти их длины, делим DA на 5 частей, DF забирает себе 4 из них, оставляя одну часть отрезку FA. Итак, DF=4/5.
Применим теорему о пропорциональных отрезках к углу ABC, стороны которого пересекают параллельные прямые DE и FC:
BE:EC=BD:DF; BE:EC=4:(4/5)=5:1. То есть точка E делит BC в отношении 5:1. Иными словами, BE - это 5/6 от BC.
Итак, BD=(4/5)BA; BE=(5/6)BC;
Переходим к нахождению площадей:
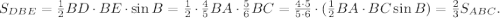
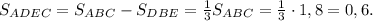
ответ: 0,6
В решении.
Пошаговое объяснение:
При каком значении x, выражение a(8a+3)²+x(a+1/3) является КУБОМ двучлена?
1) Раскрыть скобки:
a(8a+3)²+x(a+1/3) =
= а(64а² + 48а + 9) + x(a + 1/3) =
= 64а³ + 48а² + 9а + ха + х/3;
2) Рассмотреть формулу куба суммы и сравнить с полученным выражением:
(а + в)³ = а³ + 3 * а² * в + 3 * а * в² + в³;
= 64а³ + 48а² + 9а + ха + х/3;
Очевидно, что (9а + ха) = 12а, и что х = 3:
Тогда: (4а)³ + 3 * (4а)² * 1 + 3 * 4а * 1² + (1)³ =
= 64а³ + 48а² + 12а + 1³ =
= (4а + 1)³. Показатель степени =3, если плохо видно.