Вроде вот так. Надеюсь что )
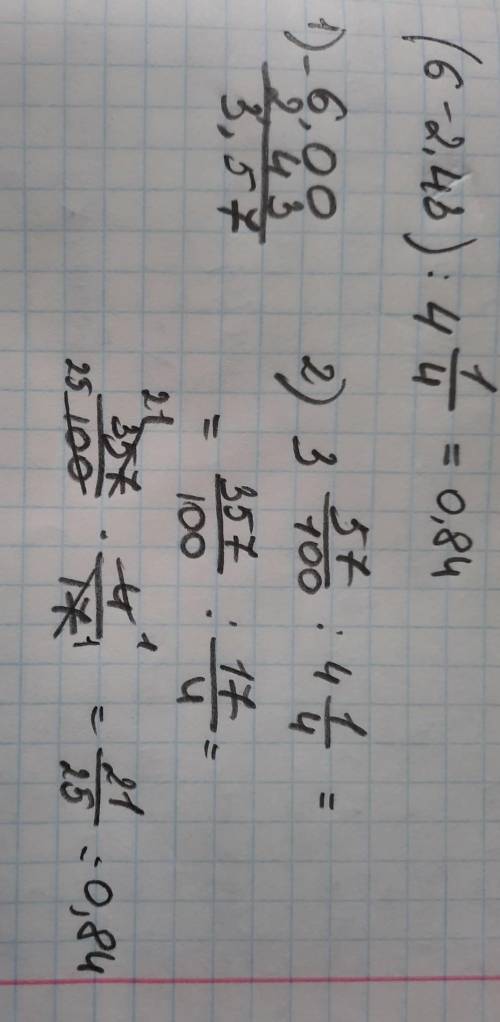
Метод Аргеландера.
Метод известен с конца XVIII века, когда немецкий астроном Ф. Аргеландер предложил достаточно простой и надежный оценки блеска с использованием степеней. За степень принимают минимальную разность в блеске двух звезд, которую в состоянии заметить наблюдатель. Только у начинающего наблюдателя «степень» колеблется, а со временем становится стабильной. В среднем одна степень соответствует 0,1m - 0,2m и является некоторой мерой чувствительности нашего глаза.
Блеск переменной определяют относительно группы звезд сравнения, отмеченной на вашей поисковой карте. Их необходимо уверенно отождествить в поле зрения бинокля или телескопа. Переменную звезду обозначают буквой V (variable), а звезды сравнения - a, b, c … в порядке уменьшения их блеска. Не забывайте фиксировать дату и время каждого сравнения.
Предположим, что Вы сравниваете постоянную звезду «а» с переменной V. Вначале присматриваемся к блеску каждой из них. Сравнение существенно затрудняется, если звезды a и V заметно различаются по цвету. Если количество степеней окажется больше 5, то необходимо использовать другую звезду сравнения, т.к. чем больше количество степеней, тем привязки становятся более нелинейными и точность сравнения падает.
Если в момент сравнения звезды a и V Вам кажутся одинаковыми по яркости, то в журнал записывают a = V. Если же звезда a ярче V на едва уловимую Вашим глазом величину, т.е. 1 степень, то в журнал заносят a1V. При более значительном различии в блеске записывают a 2 V или a 3 V и т.д.
Аналогично проводится сравнение, если другая звезда «b» слабее V.
Метод Пикеринга
Этот метод открыт в конце XIX века американским профессором астрономии Э.Ч. Пикерингом. Он основан на линейной интерполяции, т.е. нахождении промежуточного значения линейно меняющейся функции, когда известны ее значения в конечных точках интервала.
В этом случае блеск переменной звезды V также сравнивают с двумя звездами сравнения a и b, причем одна из них ярче, а вторая слабее переменной в момент сравнения. Интервал блеска между звездами сравнения условно делят на 10 частей.
После этого наблюдатель интерполирует блеск V, наблюдая попеременно 3 звезды: a, b и V.
Если при сравнении переменной V со звездой а Вы зафиксировали, что звезда V слабее на три десятых интервала a – b, то запиывают a3V7b, т.е. V ярче b на 0,7 интервала и слабее а на 0,3 интервала.
В общем виде anVmb, где n+m=10. Также возможны оценки a=V или V=b.
Метод Нейланда – Блажко
Метод открыт в XX веке голландским астрономом А.А. Нейландом и советским астрономом С.Н. Блажко. Метод является комбинированным. Содержит положительные стороны методов Аргеландера и Пикеринга.
При наблюдении используют 2 звезды сравнения, но делят интервал блесков звезд не на 10 частей, а на такое количество степеней, которое реально может оценить наблюдатель.
Если у наблюдателя сложилось впечатление, что переменная V на 2 степени слабее звезды сравнения "а" и в свою очередь она ярче “b” на 3 степени, то записывают a2V3b.
(6-2,43)=3,57
4 1/4 = 4,25
3,57:4,25=0,84
84
100