Капитан на вопрос "сколько у него в команде людей? " ответил что две пятых его команды в карауле две седьмых в работе одно четвёртая в лазарете да ещё 27 на лицо. спрашивается число людей его команды.

👇

Увидеть ответ

Ответ:

help1010100101020349

07.08.2020

х - количество человек в команде

2х/5 - каркул

2х/7 - работа

х/4 - лазарет

2х/5+2х/7+х/4+27=х

приводим к общему знаменателю 140

28*2х+20*2х+35х+3780=140х

140х-56х-40х-35х=3780

9х=3780

х=420

4,5(89 оценок)

Открыть все ответы

Ответ:

nikitos22813371

07.08.2020

Пошаговое объяснение:

1 Частные производные для F(x,y,z)=1

dFx=2x, dFy=-2y, dFz=-2z

Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(2,4,-4)

Уравнение плоскости A*x+B*y+C*z+D=0

A=Nx=2 B=Ny=4 C=Nz=-4

D=-(Nx*Mx+Ny*My+Mz*Mz)=-(2*1+4*(-2)+(-4)*2)=14

Плоскость 2x+4y-4z+14=0

Нормаль (x-1)/2=(y+2)/4=(2-z)/4

2 Частные производные для F(x,y,z)=2

dFx=2xz-2y^3, dFy=-6xy^2, dFz=12z^3+x^2

Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(0,-6,13)

Уравнение плоскости A*x+B*y+C*z+D=0

A=Nx=0 B=Ny=-6 C=Nz=13

D=-(Nx*Mx+Ny*My+Mz*Mz)=-(0*1+(-6)*1+13*1)=-7

Плоскость -6y+13z-7=0

Нормаль (1-y)/6=(z-1)/13

3. Производные на вложенном изображении.

Чтобы перейти к целым числам значения производных в т (1,1,1) домножены на 6.

Вектор нормали тогда N=(3,5,38)

Уравнение плоскости 3x+5y+38z-46=0

Нормаль (x-1)/3=(y-1)/5=(z-1)/38

Напишите уравнения касательной плоскости и нормали к заданной поверхности в точке (100,)

4,7(90 оценок)

Ответ:

АсяБру

07.08.2020

Пример смешанных дробей:

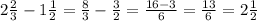
$2\frac{2}{3}-1\frac{1}{2}=\frac{8}{3}-\frac{3}{2}=\frac{16-3}{6}=\frac{13}{6}=2\frac{1}{2}$

1.нужно убрать целую часть-перевести смешанную дробь в неправильную.

2.если знаменатели разный(у нас такой же случай), то приводим к общему знаменателю( в нашем случае общ. знаменатель- 6)

3. если одинаковые, тогда решаем рациональнее- вычисляем целые и дробные части отдельно:

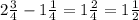
$2\frac{3}{4}-1\frac{1}{4}=1\frac{2}{4}=1\frac{1}{2}$

Пример обыкновенных дробей:

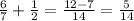
$\frac{6}{7}+\frac{1}{2}=\frac{12-7}{14}=\frac{5}{14}$

1. в данном случае, мы только приводим дроби к общ. знаменателю и далее вычисляем.

при сумме тех же дробей:

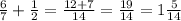
$\frac{6}{7}+\frac{1}{2}=\frac{12+7}{14}=\frac{19}{14}=1\frac{5}{14}$

2. выполняем пункт 1 и выделяем целую часть: числитель делим на знаменатель.

Пример десятичных дробей:

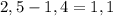2,5-1,4=1,1 -здесь можно вычитать не обращая внимания на запятую: 25-14=11, затем отделить запятую одну цифру справа налево.

ещё такой пример: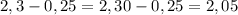 2,3-0,25=2,30-0,25=2,05 -здесь можно вычитать в столбик, только, чтобы запятая под запятой находились(смотри как это делается во вложении)