В решении.
Пошаговое объяснение:
Представьте бесконечную десятичную периодическую дробь 7,1(6) в виде обыкновенной.
Чтобы обратить смешанную периодическую дробь в обыкновенную, нужно из числа, стоящего после запятой до второго периода, вычесть число, стоящее после запятой до первого периода, и эту разность сделать числителем, а в знаменатель записать цифру 9 столько раз, сколько цифр в периоде, со столькими нулями справа, сколько цифр между запятой и первым периодом.
7,1(6) = 7 ((16-1)/90) = 7 15/90.
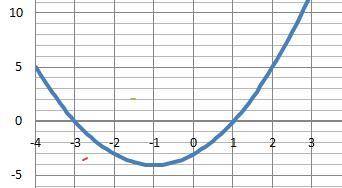
ДАНО: y(x) = x² + 2*x - 3
ИССЛЕДОВАНИЕ
1. Область определения. Непрерывная. Разрывов нет.
D(y) = (-∞;+∞) , D(y) = R.
2. Нули функции, корни квадратного уравнения.
х₁ = - 3 и х₂ = 1.
3. Интервалы знакопостоянства.
Положительна: Y>0 X∈(-∞;-3)∪(1;+∞) - вне корней.
Отрицательна: Y<0 X∈(-3;1) - между корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 2*х + 2 = 2*(x + 1) = 0
Точка экстремума: x = - 1
5 Локальный экстремум: Ymin(-1) = - 4
6. Интервалы монотонности.
Убывает: Х∈(-∞;-1) Возрастает: Х∈(1;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 2.
8. Вогнутая - "ложка" - Х∈(-∞;+∞).
9. Область значений: E(y)= [-4;+∞)
График на рисунке в приложении.
7 шоколадок
Пошаговое объяснение: