ответ:х - привезли.
2/5х-продали в 1 день.
х - 2/5х = 3/5х - осталось.
3/5х * 1/3 = 1/5х - продали во второй день.
2/5х -1/5х = 1,2
1/5х = 1,2
х = 1,2 : 1/5х
х = 6т. - яблок привезли в магазин
6 * 2/5 = 2,4 т - продали в 1 день.
6 * 1/5 = 1,2 т - продали во 2 день.
6 - 2,4 - 1,2 = 2,4 т - осталось в магазине.
Пошаговое объяснение:
вот ответ держи
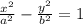 .
.

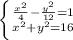
Пусть x-это количество яблок во втором магазине, тогда 3x-это количество в первом.
Составим уравнение:
3x-30=x+10
3x-x=10+30
2x=40/2
x=20
ответ:20