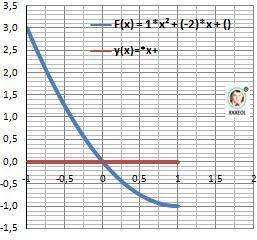
Дано: F(x) = x² -2*x , y(x)=0, а = -1,
b = 1
Найти: S=? - площадь фигуры
b = 1 - верхний предел, a = -1 - нижний предел.
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) =2*x - x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = (2)/2*x² -1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-1) = 1 + 1/3 = 4/3 (1.33)
S(b) = S(1) = 1 - 1/3 = 2/3 (0.67)
ВАЖНО! Площади с двух сторон от оси ОХ - сумма площадей.
S = S(-1) + S(1) = 4/3 + 2/3 = 2 (ед.²) - площадь - ответ
Рисунок к задаче в приложении.
Пошаговое объяснение:
Некоторые числа заключены в модуль. Вспомним, что такое модуль.
Модуль - это расстояние от начала отсчета координат до точки.
Правило: числа из модуля всегда выходят со знаком плюс.
-|24| = -24. Число вышло из модуля со знаком плюс, но перед модулем стоял знак минус. Поэтому получили -24.
|-12| = 12. Напоминаю, что числа из модуля выходят всегда со знаком плюс!
-|-7| = -7. Число -7 вышло из модуля со знаком плюс, но как назло перед модулем стоял знак минус. Поэтому -7.
-(-3) = 3. Тут уже идет раскрытие скобок. Так как перед скобкой стоит минус, в скобке знак меняется на противоположный, то есть, плюс.
Ну и осталось -9.
Теперь расставляем эти числа в порядке убывания, т.е. от большего к меньшему:
12;3;-7;-9;-24
Отрицательное число всегда меньше положительного.
Задача решена.
y=2-log₃√(9+8x-x²) ОДЗ: 9+8х-х²>0
х²-8х-9<0
х²-8х-9=0 ⇒ х₁=-1 , х₂=9 (по теореме Виета) ⇒ (х+1)(х-9)<0 + + + - - - + + +
Знаки: (-1)(9)
х∈(-1, 9)
Пересечение интервалов : (-9,9)∧(-1,9)=(-1,9)
Целые числа из этого интервала: 0,1,2,3,4,5,6,7,8.
Их сумма : 0+1+2+3+4+5+6+7+8=28