Внешний угол правильного восьмиугольника равен 45 градусам.
Т. к.
1) 180 * (8 - 2) = 1080 - сумма внутренних углов восьмиуголиника.
2) 1080 / 8 = 135 градусов - один угол
3) 180 - 135 = 45 градусов - внешний угол
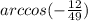
Пошаговое объяснение:
Составим вектора имеющие начало в точке A, а конец в B или C:
AB = {2, -3, 6}
AC = {6, 2, -3}
Скалярное произведение:
AB * AC = 12 - 6 - 18 = -12
AB*AC ≠ 0, значит вектора не перпендикулярны
Найдем длины векторов:
|AB| =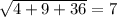 
|AC| =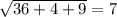 
Пусть 
- искомый угол (он же угол между векторами АВ и АС)
Приравняем скалярное произведение через длины к скалярному произведению через координаты:
|AB| * |AC| * cos 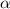= -12
Выразим косинус угла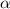
cos =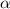 
= 
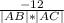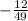
Выразим 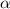через обратную тригонометрическую функцию
=
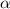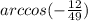
Примечание:
Найти этот арккосинус можно с калькулятора, окажется что наш искомый угол равен примерно 104°. Также это проверяется построением треугольника в системе координат.
ответ: 45