На конструкцию можно смотреть с 4 сторон: спереди, слева, сзади и справа. Просчитаем максимально возможное число кубиков в каждом случае, зная что максимальные количества кубиков в башнях по линиям соответственно равны 2, 4, 1, 3.
1. Смотрим спереди: соответствующие линии показаны на картинке. Максимальные количества башен по линиям соответственно равны 3, 1, 2, 3.
Итого: 2·3+4·1+1·2+3·3=6+4+2+9=21
2. Смотрим слева. Максимальные количества башен по линиям соответственно равны 2, 2, 2, 3.
Итого: 2·2+4·2+1·2+3·3=4+8+2+9=23
3. Смотрим сзади. Максимальные количества башен по линиям соответственно равны 3, 2, 1, 3.
Итого: 2·3+4·2+1·1+3·3=6+8+1+9=24
4. Смотрим справа. Максимальные количества башен по линиям соответственно равны 3, 2, 2, 2.
Итого: 2·3+4·2+1·2+3·2=6+8+2+6=22
Максимальное количество при взгляде сзади - 24.
ответ: 24
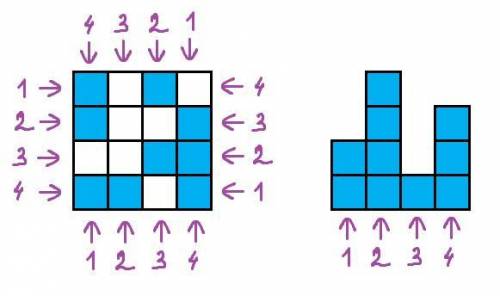
В решении.
Пошаговое объяснение:
Определите вид зависимости величин и решите задачу с
составления пропорции.
С одинаковых труб бассейн заполняется водой за 25 минут. За сколько минут можно заполнить бассейн с таких труб?
Пропорция:
8 (труб) - 25 (минуты)
10 (труб) - х (минут)
Зависимость обратно пропорциональная ( чем больше труб, тем меньше времени понадобится):
8/10 = х/25
По основному свойству пропорции (произведение её крайних членов равно произведению средних членов):
х=8*25:10
х=20 (минут).