Пусть все 290 слагаемых равны по 2. Тогда их сумма равна 290·2=580, что меньше 2020. Значит, среди слагаемых есть число, большее 2.
Пусть каждое из 290 слагаемых равно по 2 или по 3. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·3=870, что меньше 2020. Значит, среди слагаемых есть число, большее 3.
Пусть каждое из 290 слагаемых равно по 2, по 3 или по 5. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·5=1450, что меньше 2020. Значит, среди слагаемых есть число, большее 5.
Пусть каждое из 290 слагаемых равно по 2, по 3, по 5 или по 7. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·7=2030. Это больше, чем 2020, значит такой вариант можно рассматривать далее.
Максимальная сумма получается при суммировании 290 чисел, каждое из которых равно по 7. Как видно, максимальная сумма больше требуемой на 10. Тогда, можно уменьшить некоторые слагаемые в этой сумме. Например, уменьшить 2 слагаемых на 5. Получим сумму вида:
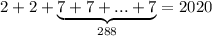
Наибольшим слагаемым является число 7.
ответ: 7
1)Это прямая с выбранными на ней началом отсчета, направлением и единичным отрезком.2)Прямая, на которой выбраны начало отсчета, положительное направление и единичный отрезок, называется координатной прямой. На координатной прямой каждому рациональному числу соответствует единственная точка. Число, соответствующее данной точке на координатной прямой, называется координатой этой точки.3)число из пары чисел, которые при сложении дают 0 ◆ Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.4)Очень большое количество, число кого-чего-н 5)НЕ ЗНАЮ 6) НЕ ЗНАЮ 7)Модулем положительного числа называется само число, модулем отрицательного числа называется противоположное ему число, модуль нуля - нуль. Противоположными называются числа, которые отличается только знаком. Если число положительное, то противоположное ему отрицательное число и наоборот. 8) НЕ ЗНАЮ 9) НЕ ЗНАЮ 10) ТОЖЕ НОЛЬ. 11) НЕ ЗНАЮ 12) НЕ ЗНАЮ(сорри)
10 раз
Пошаговое объяснение:
Знаток Михаил Скипский, Тур-де-Ски, чистые носки, долгие скитания, эллиптические куски, исковые иски к буквам «кси», скисшие щи, лески, зажатые в тиски, диски куплены в магазине «Дикси».