Задача на подобие треугольников (коэффициенты подобия).
В первом треугольнике - стороны 4 см, 6 см и 9 см.
Во втором треугольнике - стороны X см, Y см и 36 см.
*в первом треугольнике самая большая сторона - 9 см, во втором треугольнике - 36 см (бóльшая сторона одного треугольника соотносится с большей стороной второго треугольника).
Значит они относятся с каким-то коэффициентом подобия (раз по условию треугольники подобны): (бóльшая сторона большего треугольника разделить на бóльшую сторону меньшего треугольника).
Соответственно, теперь по этому коэффициенту можно найти оставшиеся стороны:
Первая сторона - см
Вторая сторона - см
Третья сторона - см (по условию)
Периметр большего треугольника: см.
*дополнительно это можно и проверить. Периметры подобных треугольников соотносятся как коэффициент подобия:
Периметр меньшего треугольника: см
Тогда поделив периметр большего треугольника на меньшего треугольника мы будем должны получить этот самый коэффициент подобия (то есть 4): - значит задача решена верно!
1.чтобы сложить два числа с одинаковыми знаками надо поставить их общий знак и приписать модулей. примеры:(-3) + (-6) = -(3 + 6) = -9; (+3) + (+5) = +(3 + 5) = +8 2. Чтобы сложить два числа с разными знаками и разными модулями нужно поставить знак числа большего приписать к нему разность меньшего. примеры: -2+1 = -1; 5+ (-3)=2. 3. Сумма противоположных чисел равна нулю. примеры:-2+2=0; -8+8=0. 4. Если одно из слагаемых равно нулю то сумма равна второму слагаемому. примеры: 0+2=2; 22+0=22 Приведите по два примера на каждое правило
Задача на подобие треугольников (коэффициенты подобия).
В первом треугольнике - стороны 4 см, 6 см и 9 см.
Во втором треугольнике - стороны X см, Y см и 36 см.
*в первом треугольнике самая большая сторона - 9 см, во втором треугольнике - 36 см (бóльшая сторона одного треугольника соотносится с большей стороной второго треугольника).
Значит они относятся с каким-то коэффициентом подобия (раз по условию треугольники подобны):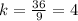
(бóльшая сторона большего треугольника разделить на бóльшую сторону меньшего треугольника).
Соответственно, теперь по этому коэффициенту можно найти оставшиеся стороны:
Первая сторона -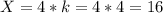
см
Вторая сторона -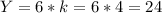
см
Третья сторона -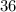
см (по условию)
Периметр большего треугольника:
см.
*дополнительно это можно и проверить. Периметры подобных треугольников соотносятся как коэффициент подобия:
Периметр меньшего треугольника: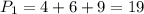
см
Тогда поделив периметр большего треугольника на меньшего треугольника мы будем должны получить этот самый коэффициент подобия (то есть 4):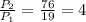
- значит задача решена верно!
ответ: 76 см.