Вариант Б2
1) Сумма смежных углов равна 180 градусов.
Пусть угол 1 будет - х , а угол второй х - 50.
х + х -50 = 180
2х = 230
х = 115
угол 2 будет 115-50 = 65 (градусов)
2) Сумма смежных углов равна 180 градусов.
Если сумма 21 градус,то эти углы вертикальные(а их 2 значит делим на 21:2 = 10,5
Смежный угол будет 180 - 10,5 = 169,5
ответ : 169,5 , 10,5 ; 169,5 , 10,5.
3) Угол АОВ+угол ВОС=180 (по теореме о смежных углах)
ВОС = 100 градусов
Если угол DO перпендикулярен прямой АС , то DOC = 90 (градусам).
Значит BOC = 100 - 90 = 10 градусов.
ответ : 10 градусов
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
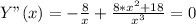
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении

Прямая y=4x+5 касается параболы y=x²+bx+c в точке с абсциссой x=-2. Найдите сумму b+c
В точке х = -2 угловой коэффициент касательной к параболе равен у'(-2)
Производная
y' =(x²+bx+c)'=2x+b
в точке х=-2
k = y'(-2) = 2·(-2)+b =-4+b
Угловой коэффициент k касательной мы уже знаем из уравнения прямой y = 4x + 5.
Угловой коэффициент k=4
Поэтому можно записать
-4+b=4
b=8
Получили уравнение параболы
y = x² + 8x + с
Зная общую точку касательной и параболы при х =-2 найдем значение ординаты у для касательной
y(-2)=4·(-2)+5=-8+5=-3
и для параболы
y(-2)=(-2)²+8·(-2)+с=4-16+с=-12+с
Так как эта точка общая для касательной и параболы то можно записать
-12+с=-3
с=12-3=9
Запишем окончательно уравнение параболы
y = x²+8x+9
b=8 c=9
b+с=8+9=17
ответ : b+c=17