log(1 + 1/(x + 1)²) (x² + 3x + 2)/(x² - 3x + 4) ≤ 0
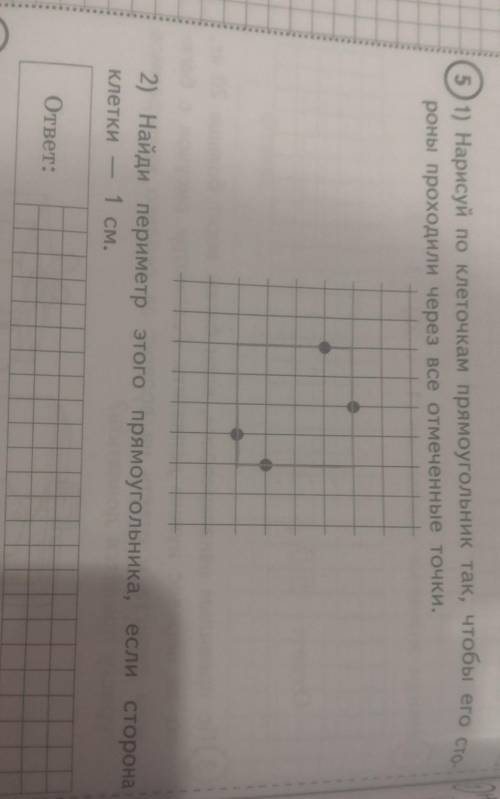
одз
1 + 1/(x + 1)² > 0 x ∈ R
1 + 1/(x + 1)² ≠ 1 x ∈ R
(x + 1) ≠ 0 x ≠ -1
(x² + 3x + 2)/(x² - 3x + 4) > 0
x² + 3x + 2 = 0 D = 9 - 8 = 1 x12 = (-3 +- 1)/2 = -2 -1
x² - 3x + 4 = 0 D = 9 - 16 < 0 x∈ R
(x + 1)(x + 2) > 0
x∈ (-∞, -2) U (-1, +∞)
log(1 + 1/(x + 1)²) (x² + 3x + 2)/(x² - 3x + 4) ≤ log(1 + 1/(x + 1)²) 1
1 + 1/(x + 1)² > 1 всегда
(x² + 3x + 2)/(x² - 3x + 4) ≤ 1
(x² + 3x + 2)/(x² - 3x + 4) - 1 ≤ 0
(x² + 3x + 2 - (x² - 3x + 4)) ≤ 0
знаменатель отбрасываем (x² - 3x + 4) он всегда >0
(x² + 3x + 2 - x² + 3x - 4) ≤ 0
6x - 2 ≤ 0
x ≤ 1/3
x∈ (-∞, -2) U (-1, 1/3]
В первой бочке изначально было 623 литра, а во второй - 626 литров
Пошаговое объяснение:
Пусть это кол-во бензина, когда в обеих бочках было его поровну, тогда
в первой бочке изначально было х + 25, а во второй х + 18. Всего в бочках было изначально (х + 25) + (х + 18) = 1239
2х = 1239 - 18 - 25
2х = 1196
х = 598(л) - количество бензино в кажой из бочках после сливания
598 + 25 = 623(л) - было в первой бочке
598 + 18 = 616(л) - было во второй бочке
ответ: в первой бочке изначально было 623 литра, а во второй - 626 литров