
Пошаговое объяснение:
1) Докажите, что функция F(x) является первообразной для функций f(x), если:
а) F(x)=x^3+4x^2-5x+7 и f(x)=3x^2+8x-5, x-все числа
б) F(x)=3x^4-lnx и f(x)=12x^3-1/x, x>0
2) Найдите первообразную для функций:
а) f(x)=2/x^3+cosx, x неравен 0
б) f(x)=3e^x, x -все числа
3) Найдите ту первообразную F(x) для функций f(x)=3x^2+4x, график которой через точку A(1;5).
4) Вычислите площадь фигуры, ограниченной линиями y=x^2 и y=9
5) Вычислите y=x^2-4x+2 и y=-x^2+6x-6
Решите хоть одно задание, за рание
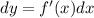 или
или 

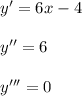


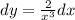
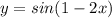




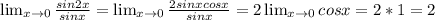
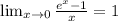
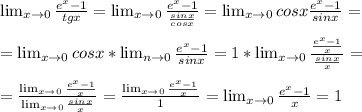
ответ на фоте
Пошаговое объяснение:
Зделай лучший ответом если я тебе памагла