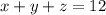, то избавимся от этого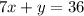
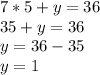
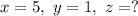
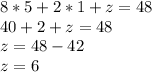
Пошаговое объяснение:
Обозначим через х число дней, за которые была прочитана книга.
В условии задачи сказано, что ученик прочитал книгу на 4 дня раньше запланированного срока, следовательно, ученик собирался прочитать книгу за х + 3 дня.
Также известно, что в книге 180 страниц и каждый день ученик читал на 10 страниц больше, чем предполагал, следовательно, можем составить следующее уравнение:
180/(х +3) +10 =180/х.
Решаем полученное уравнение:
18/(х +3) + 1 = 18/х.
18х + х * (х +3) =18 * (х + 3);
18х + х^2 + 3x = 18х + 54;
х^2 + 3x - 54 = 0;
решаем квадратное уравнение: х1=6, х2=-9, следовательно книга была прочитана за 6 дней.
1) 4√3-4>3х(1-√3)
-4(1-√3)>3х(1-√3)
3х>-4
Х>-4/3
2) √3+y√6<y+3√2
√6y-y<3√2-√3
(√6-1) y<√3(√6-1)
y<√3
3) (3√10-9√2)x<4(3√2-√10)
(3√10-9√2) x>-4(√10-3√2) | : 3√10-9√2
x<(-4(√10-3√2))/(-3(√10-3√2))
x>4/3
4) √3(1-y)>3-2y
√3-√3y>3-2y
-√3y+2y>3-√3
(-√3+2)y>3-√3
y>3/(-√3+2)-√3/(-√3+2)
y>3+√3