Пошаговое объяснение:
16(-1/8+2 1/6-2 1/2)=
16(-1/8+13/6-5/2)=
=16((-3+52-60)/24)=
=16(-11/24)= - 22/3= - 7 1/3
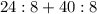
повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение:
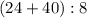
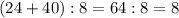В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на , то и их сумма делится на .
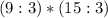
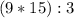
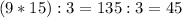
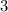,то их произведение делится на 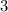" доказанным.
1:8=0,125 21:6 =3,5 21:2=10,5 0,125+3,5-10,5= -6,875
16-6,875=9,125