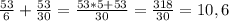 м
м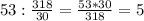 дней
дней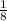 работы, 2-й за день выполнит
работы, 2-й за день выполнит 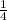 . Тогда, работая совместно, они выполнят
. Тогда, работая совместно, они выполнят 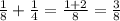
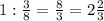 дня.ответ просят выразить в часах. Интересно, ведь не круглые сутки они копают. Если формально (хоть это не реально), то в сутках 24 часа 1/3 сут=8ч
дня.ответ просят выразить в часах. Интересно, ведь не круглые сутки они копают. Если формально (хоть это не реально), то в сутках 24 часа 1/3 сут=8ч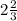 сут=
сут=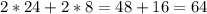 часа
часа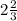 рабочих дня это будет
рабочих дня это будет 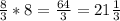 часов
часов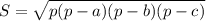 (1)
(1)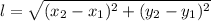 (2)
(2)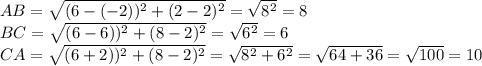
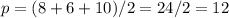
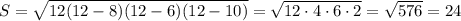
x = 1, y=5 или x=5, y=1
Пошаговое объяснение:
Заменяешь x+y на t.
t^2-7t+6=0
t+xy=11.
Решаешь первое уравнение через дискриминант или теорему Виета.
Корни получаются 6 и 1. Это значения x+y. Рассмотрим сначала первый вариант, когда x+y=6.
t=6
t+xy=11.
xy=5. Выразим из x+y=6 любую переменную, например x. x=6-y.
Подставим в xy=5.
(6-y)y=5
6y-y^2=5
y^2-6y+5=0
Находишь корни через дискриминант или теорему Виета уже для этого случая.
Корни получаются: 1;5
При y=1 x=5 и при y=5 x=1.
Рассмотрим второй случай, когда x+y=1 (Оно же t=1).
Подставим в t+xy=11.
xy=10
Выразим любую переменную.
x=1-y
(1-y)y=10
y-y^2=10
y^2-y+10=0
У этого выражения нет корней, т.к. дискриминант отрицательный, следовательно ответом будет (1;5),(5;1)