Пусть все 290 слагаемых равны по 2. Тогда их сумма равна 290·2=580, что меньше 2020. Значит, среди слагаемых есть число, большее 2.
Пусть каждое из 290 слагаемых равно по 2 или по 3. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·3=870, что меньше 2020. Значит, среди слагаемых есть число, большее 3.
Пусть каждое из 290 слагаемых равно по 2, по 3 или по 5. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·5=1450, что меньше 2020. Значит, среди слагаемых есть число, большее 5.
Пусть каждое из 290 слагаемых равно по 2, по 3, по 5 или по 7. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·7=2030. Это больше, чем 2020, значит такой вариант можно рассматривать далее.
Максимальная сумма получается при суммировании 290 чисел, каждое из которых равно по 7. Как видно, максимальная сумма больше требуемой на 10. Тогда, можно уменьшить некоторые слагаемые в этой сумме. Например, уменьшить 2 слагаемых на 5. Получим сумму вида:
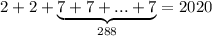
Наибольшим слагаемым является число 7.
ответ: 7
61 км/ч скорость автобуса
77 км/ч скорость грузовой машины
Пошаговое объяснение:
Пусть скорость автобуса = х км/ч, тогда скорость грузовика = (х+16) км/ч
1. х + х + 16 = 2х + 16 (км/ч) - скорость сближения автобуса с грузовой машиной
Автобус и грузовая машина были в пути 4 часа каждый и проехали 552 км
Составим уравнение:
2. 4(2х+16) = 552
8х + 64 = 552
8х = 552 - 64
8х = 488
х = 488/8
х = 61 (км/ч) скорость автобуса
61 + 16 = 77 (км/ч) скорость грузовой машины
Проверим:
(61+77)*4 = 552
138*4 = 552
552 = 552 (км) - Автобус и грузовая машина за 4 часа проехали 552 км
(1+3)/1 = 1+3 = 4.
Пошаговое объяснение:
Початкова умова: (√5+3√5)/√5
1) Дія в дужках: винесемо √5 як спільний множник, тоді маємо:
√5(1+3)
2) Дія з дробом: після винесення √5 за дужки дріб має вигляд:
(√5(1+3))/√5
І в чисельнику, і в знаменнику маємо √5, тому цей вираз скорочується, і ми отримуємо:
(1+3)/1 = 1+3 = 4.