![\sqrt[3]{5}](/tpl/images/4363/3558/dada8.png) - 4
- 4![\sqrt[8]{7}](/tpl/images/4363/3558/c8c15.png) )'
)'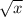 - 7x^5 +3cos45°)'
- 7x^5 +3cos45°)'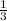 x)'
x)'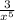 )'
)'![\sqrt[3]{x^7}](/tpl/images/4363/3558/ff640.png) -2
-2![\sqrt[4]{x}](/tpl/images/4363/3558/846fb.png) +
+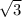 )'
)'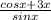 ) '
) '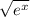 )'
)'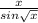 )'
)'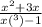 )'
)'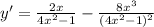

1
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
вероникасмс
04.09.2016
Математика
1 - 4 классы
+5 б.
ответ дан
задай множество перечислением: а) А-множество букв в слове крот б)В-множество однозначных чисел, меньших 5; в)С - множество двухместных чисел, кирпичных 10;г) D-множество трехзначных чисел,больших 603,но мегьших608.
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
ответ, проверенный экспертом
3,2/5
6

xERISx
главный мозг
3 тыс. ответов
3.1 млн пользователей, получивших
Задай множество перечислением:
а) А - множество букв в слове крот
А = {к; р; о; т}
б) В - множество однозначных чисел, меньших 5
Если речь идёт о натуральных числах :
В = {1; 2; 3; 4}
Если речь идёт о целых числах :
В = {-9; -8; -7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4}
в) С - множество двузначных чисел, кратных 10
Если речь идёт о натуральных числах :
С = {10; 20; 30; 40; 50; 60; 70; 80; 90}
Если речь идёт о целых числах :
С = {0; 10; 20; 30; 40; 50; 60; 70; 80; 90}
г) D - множество трехзначных чисел,больших 603,но меньших 608
D = {604; 605; 606; 607}
1
2
3
4
5
6
7
8
9