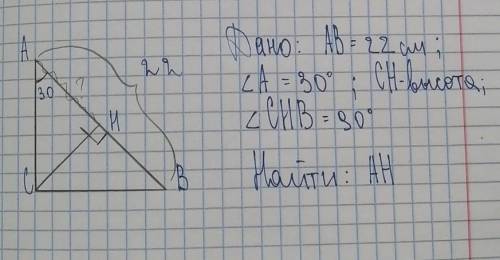
1) длина стороны квадрата 28 м
2) длина радиуса полукругов = 14 м
3) длина декоративного забора 9408 м
Пошаговое объяснение:
клумба получается примерно как на рисунке
здесь видно, что площадь клумбы S = S₁ + 4S₂
где S₁ - площадь квадрата S₂ - площадь полукруга
при этом сторона квадрата = диаметру круга = 2*радиус круга
пусть а - сторона квадрата, тогда d = a, r=1/2 a
теперь формулы
S₁ (площадь квадрата) = а²
S₂ (площадь круга) = 
L (длина окружности) = 
для площади круга нам нужно площадь квадрата + 4 площади полукруга или 2 площади круга, получим
1960 = S₁ + 2 S₂ = a² + 2
решаем относительно а и получим а=28 (м)
теперь считаем длину забора
L = 4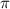
d² = 4*3*28² = 4*3* 784 = 9408 (м)
1) длина стороны квадрата 28 м
2) длина радиуса полукругов = 14 м
3) длина декоративного забора 9408 м
3)все 4 функции вида y = kx + b. если b > 0, то прямая соприкасается с осью ординат выше оси абсцисс, а если b < 0, то прямая соприкасается с осью ординат ниже оси абсцисс. значит, графики a и b соответствуют уравнениям 2 и 3, а графики c и d соответствуют уравнениям 1 и 4. определим теперь конкретно какой график к какому уравнению подходит. рассмотрим уравнение, в котором k = 2 y = 2x + 5, причём x = = 2,5. значит, прямая проходит через точку абсцисс 2,5. рассмотрим уравнение, в котором k = 1 y = x - 5, из свойств числового коэффициента b следует, что график проходит через точку ординат -5, а из формулы y = a(x - m)² следует, что точка соприкосновения оси абсцисс и прямой смещена вправо на 5. проведя аналогичные рассуждения с остальными двумя уравнениями и их графиками, придём к выводу, что1) - c2) - a3) - b4) – d
ответ: AH=16,5 см
Пошаговое объяснение:
1. ΔBAC(∠C=90°):
∠B=90°-∠A=90°-30°=60°(Сумма острых углов прямоугольного треугольника равна 90 градусам)
CB=1/2 AB=22/2=11см(Катет CB, лежащий против угла в 30°, равен половине гипотенузы AB)
2. ΔCHB(∠CHB=90°):
∠BCH=90°-∠B=90°-60°=30°(Сумма острых углов прямоугольного треугольника равна 90 градусам)
HB=1/2 CB=11/2=5,5 см(Катет HB, лежащий против угла в 30°, равен половине гипотенузы CB)
3. ΔBAC(∠C=90°):
AH=AB-HB=22-5,5=16,5 см