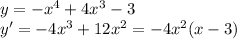
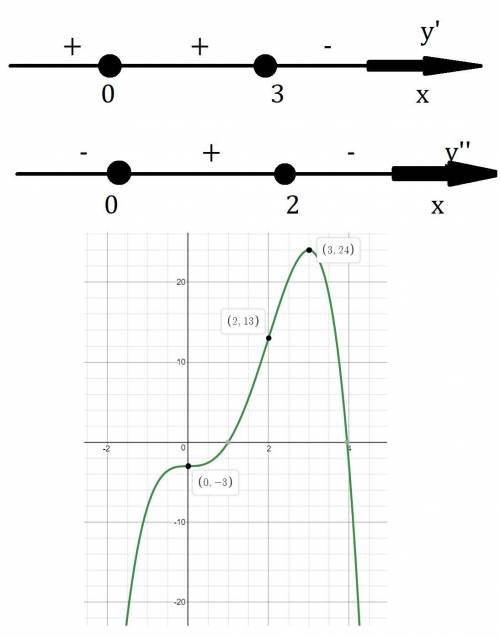
Как видно производная обращается в ноль при x=3 и x=0 это критические точки, используем метод интервалов, для определения знака производной на промежутках.
При x=0, производная не меняет знак, значит это не экстремум функции. При x=3, производная меняет знак с плюса на минус, значит это минимум функции.
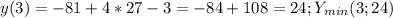
На (-∞;0)∪(0;3) функция растёт.
На (3;+∞) функция убывает.
Функция общего вида (не обладает чётность или нечётностью)
Найдём точки перегиба функции.
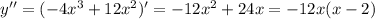
x=0 и x=2 это точки перегиба.
На (-∞;0)∪(2;+∞) функция выпукла вверх.
На (0;2) функция выпукла вниз.
Найдём координаты всего чего ещё не нашли.
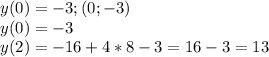
Можем строить.
Наименьшее значение (-∞;-∞) и (+∞;-∞)
Наибольшее значение (3;24)
дана эта формуланужно исследовать её на монотонностьнайти н" />
1. Не существует такого натурального числа которое являлось бы делителем любого натурального числа.Неверно
2. Одним из кратных натурального числа m является само число m Верно
3. Любое натуральное число имеет бесконечно много делителей Верно
4. Если число делится без остатка на 10, то оно не кратно 2 Неверно
5. Если число кратно 9, то оно делится без остатка на 3 Верно
6. Разность двух нечетных чисел-число нечетное Неверно
7. Если знаменатель одной из двух дробей кратен знаменателю второй, то он является наименьшим общим знаменателем этих двух дробей. Неверно
8.Если число кратно 9, то оно делится без остатка на 3. Верно