ответ: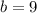 
Пошаговое объяснение:
Подставляем координаты точки в уравнение прямой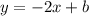 
:
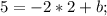
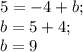
Расположим делители числа k в порядке возрастания (естественно, если такие делители существуют).
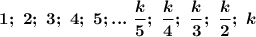
Пусть a < b.
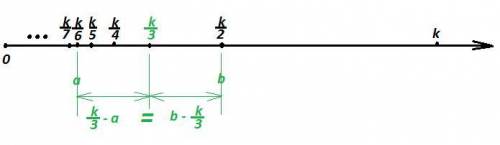
Так как различные натуральные делители a и b расположены на одинаковом расстоянии от числа k/3, то расположены они по разные стороны от числа k/3
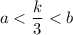
На числовой оси правее числа k/3 ( то есть больше числа k/3) расположены только два делителя : само число k и k/2.
b = k не подходит по условию, так как делитель a тогда отрицательный
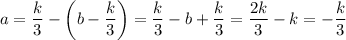
Остаётся единственный вариант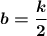 
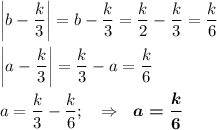
Так как у делителей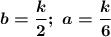 
общий знаменатель равен 6, то олимпиадными будут все числа, кратные 6. Тогда олимпиадных чисел, не превосходящих 2018:
2018 : 6 = 336,(3) - 336 чисел
Проверка :
k=6; b=3; a=1; |1-2|=|3-2| =1
k=12; b=6; a=2; |2-4|=|6-4| =2
k=18; b=9; a=3; |3-6|=|9-6| =3 ...
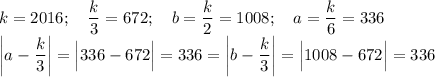
ответ : 336 чисел
ответ:Решение:
$\frac{1}{4}\cdot\left(1\frac{1}{2}+\frac{1}{8}\right)^2+1.56=\frac{1}{4}\cdot\left(1\frac{5}{8}\right)^2+1.56=\frac{1}{4}\cdot\frac{169}{64}+1.56=\frac{169}{256}+1.56=2\frac{1409}{6400}=2\frac{1409}{6400}=2.22015625$
1 1 2 + 1 8 = 1 + 1 2 + 1 8 = 1 + 1 · 4 2 · 4 + 1 · 1 8 · 1 = 1 + 4 8 + 1 8 = 1 + 4 + 1 8 = 1 + 5 8 = 1 5 8 = 1.625
(1 5 8 )2 = 169 64
1 4 × 169 64 = 1·169 4·64 = 169 256 = 0.66015625
169 256 + 1.56 = 169 256 + 1 56 100 = 1 + 169 256 + 56 100 = 1 + 169 · 25 256 · 25 + 56 · 64 100 · 64 = 1 + 4225 6400 + 3584 6400 = 1 + 4225 + 3584 6400 = 1 + 7809 6400 = 1 +
Пошаговое объяснение:
9
Пошаговое объяснение:
5=-4+d
-d= -5-4
-d=-9
d=9
проверяем
5=-4+9
5=5