Пошаговое объяснение:
941.
1. 18/85 ÷27/68 ·45/28 ÷12/77=18/85 ·68/27 ·45/28 ·77/12=2/5 ·4/3 ·15/4 ·11/4=(3·11)/(3·2)=11/2=5,5
1.1. 18/85 ·68/27=2/5 ·4/3
1.2. 45/28 ·77/12=15/4 ·11/4
2. 80/81 ÷40/63 ·27/28 ÷3/20=80/81 ·63/40 ·27/28 ·20/3=20/3 ·1/7 ·21/2=(10·3)/3=10
2.1. 80/81 ·27/28=20/3 ·1/7
2.2. 63/40 ·20/3=21/2
3. 99/160 ÷33/40 ·20/27 ÷5/81=99/160 ·40/33 ·20/27 ·81/5=11/8 ·1/3 ·8/11 ·27=27/3=9
3.1. 99/160 ·20/27=11/8 ·1/3
3.2. 40/33 ·81/5=8/11 ·27
4. 24/37 ÷27/74 ÷32/45 ·14/15=24/37 ·74/27 ·45/32 ·14/15=8·2/9 ·3/16 ·7=2/9 ·3/2 ·7=7/3=2 1/3
4.1. 24/37 ·74/27=8·2/9
4.2. 45/32 ·14/15=3/16 ·7
942.
x+8 5/6=10 1/3; x=10 2/6 -8 5/6=9 8/6 -8 5/6=1 3/6=1 1/2=1,5
11 7/9 +y=13 1/18; y=13 1/18 -11 14/18=12 19/18 -11 14/18=1 5/18
x-24 2/7=16 3/8; x=16 21/56 +24 16/56=40 37/56
60 2/5 -y=57 3/4; y=60 8/20 -57 15/20=59 28/20 -57 15/20=2 13/20=2,65
2 2/9 ·x=1 1/2; x=3/2 ·9/20=27/40=0,675
1 13/75 ·y=2/3; y=2/3 ·75/88=25/44
x ÷35/36=1 1/20; x=21/20 ·35/36=7/4 ·7/12=49/48=1 1/48
24/35 ÷y=1 5/49; y=24/35 ·49/54=4/5 ·7/9=28/45
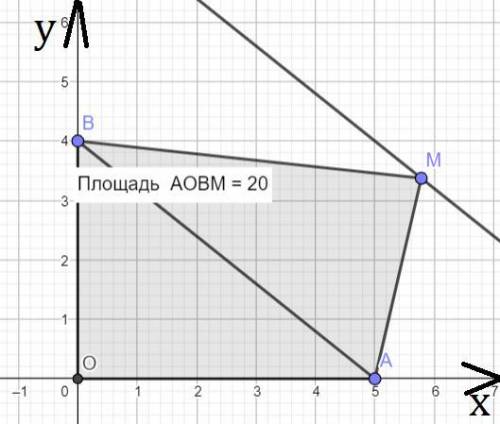
Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
4=a·o+t ⇒ t=4; 0=a·5+t ⇒ a=-4/5=-0,8
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-0,8x+4.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=20, S(AOB)=AO·OB/2=10.
Тогда S(BMA)=10.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -0,8
ответ: -0,8.
6х + 2х + 2,352 = 4,2
8х = 4,2 - 2,352
8х = 1.848
х = 1.848 : 8
х = 0,231
Пошаговое объяснение: