Відповідь:
1)6*6*6=216 (см^3) - объем куба
2)18:3=6 (см) - ширина параллелепипеда
3)18*6*х=216
х=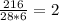
Покрокове пояснення:
t - время, которое ехал от А до С мотоциклист и от С до В автомобиль
t+1,5 - время которое ехал до С автомобиль
300: (t+t+1,5) = 300: (2t+1,5) - скорость автомобиля
расстояние от А до С - 60*t или 300 * (t+1,5) : (2t+1,5)
Приравняем и получим уравнение:
Приведем к общему знаменателю и с учетом того, что знаменатель не может быть равен 0 получим:
60t (2t+1,5) = 300 (t+1,5)
120t^2+90t=300t+450
120t^2-210t-450=0
12t^2-21t-45=0
4t^2-7t-15=0
Решим это уравнение, получим 2 корня t=-1,25 и t=3
t=-1,25 - не подходит, т. к. время не может быть меньше 0.
Значит расстояние от А до С равно 60*3 = 180 (км)
С одного сайта взял
а) Обозначим точки пересечения лучей с отрезком BM — буквами P и R (см. рисунок), и пусть O — точка пересечения диагоналей параллелограмма, а N — точка пересечения луча AP и прямой BC.
Точка R делит медиану BM треугольника ABD в отношении 2 :1 считая от B. Следовательно, R лежит на медиане AO этого треугольника, то есть луч AR содержит диагональ AC .
б) Пусть L — точка пересечения AN и BD. Нужно найти площадь четырёхугольника LNCO. Пусть площадь параллелограмма равна S . Площадь треугольника BOC равна Найдём площадь треугольника BNL . Из подобия треугольников BPN и MPA следует, что
откуда
Теперь из подобия треугольников BNL и DAL следует, что их соответствующие высоты относятся как 1:4 , а поэтому высота треугольника BNL, проведённая к BN, составляет высоты параллелограмма, проведённой к стороне BC.
Поэтому
Следовательно, площадь четырёхугольника LNCO равна
Пошаговое объяснение:
2 см.
Пошаговое объяснение:
1) 18:3=6(см.)-ширина
2) 18×6=108(см.)-плошадь
3) 6³=216(см.³)-объем
4) 216:108=2(см.)-высота