Пошаговое объяснение:
1) 5,22+7,78=13
13+9,694=22,694
2) 32,64+27,36=60
60+8,85=68,85
3) 6,63+7,37=14
2,451+3,449=5,9
14+5,9=19,9
4) 5,415+6,585=12
3,782+4,218=8
12+8=20
Эта задача может решаться двумя геометрическим и векторным надо было указать в задании).
Геометрический.
Если мы перенесём заданный отрезок А1С1 точкой А1 в точку А, то получим плоский угол САД1 между заданными отрезками.
Решим треугольник АСД1 по теореме косинусов.
Находим длины сторон.
АС = √(4² + 8²) = √(16 + 64) = √80 = 4√5.
АД1 = √(3² + 4²) = √(9 + 16) = √25 = 5.
Д1С = √(3² + 8²) = √(9 + 64) = √73.
cos A = (80 + 25 - 73)/(2*4√5*5) = 32/(40√5) = 0,35777.
Угол А = САД1 = arc cos 0,35777 = 1,2049 радиан или 69,0366 градуса.
ответ: угол между отрезками AD1 и A1C1 равен 69,0366 градуса.
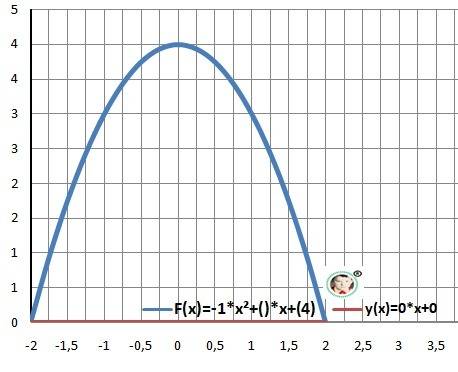
Дано: F(x)=- x²+4, y(x)=0
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков.
x²-4 = 0 - квадратное уравнение
a = -2- верхний предел, b = 2- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = -4 + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
F(x) = -4*x + 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-2) = 8 -2,67 = 5,33
S(b) = S(2) = -8 +2,67 = -5,33
S = S(2)- S(-2) = 10,66 - площадь
Рисунок к задаче в приложении.
б)
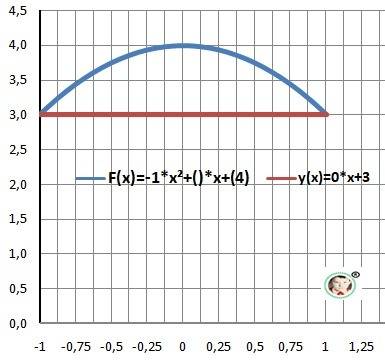
Дано: F(x)= - x² +4, y(x)= 3
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков.
x² - 1=0 - квадратное уравнение
a = -1- верхний предел, b = 1- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = -1 + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
F(x) = -x+ 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-1) = 1 - 0,33 = 0,67
S(b) = S(1) =-1 +0,33 = -0,67
S = S(1)- S(-1) = 1,34 - площадь
Рисунок к задаче в приложении.
Пошаговое объяснение:
1) 5,22 + 7,78 + 9,694 = 13 + 9,694 = 22, 964
2) 32,64+27,36 + 8,85 = 60 + 8,85 = 68,85
3) 6,63 + 7,37 + 2,451 + 3,449 = 14 + 5,9 = 19,9
4) 3,782 + 4,218 + 5,415 + 6,585 = 8 + 12 = 20