Question

с математикой , это дкр Нужен ответ с решениями и этапами
Заранее большое

Answer 1

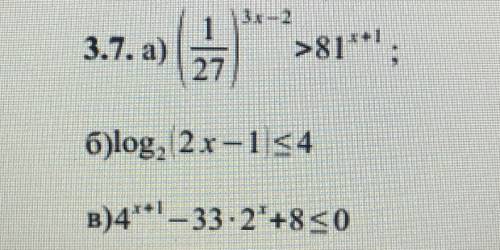
$log_{2}(2x - 1) \leqslant 4 \\ log_{2}(2x - 1) \leqslant 4,x \frac{1}{2} \\ 2x - 1 \leqslant {2}^{4} \\ 2x - 1 \leqslant 16 \\ 2x \leqslant 16 + 1 \\ 2x \leqslant 17 \\ x \leqslant \frac{17}{2} ,x \frac{1}{2} \\ x∈( \frac{1}{2} ; \frac{17}{2} ]$

${ \frac{1}{27} }^{3x - 2} {81}^{x + 1} \\ {3}^{ - 9 + 6} {3}^{4x + 4} \\ - 9x + 6 4x + 4 \\ - 9x - 4 4 - 6 \\ - 13x - 2 \\ x < \frac{2}{13}$

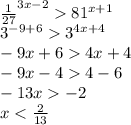
${4}^{x + 1} - 33 \times {2}^{x} + 8 \leqslant 0 \\ {4}^{x} \times 4 - 33 \times {2}^{x} + 8 \leqslant 0 \\ ( { {2}^{2} )}^{x} \times 4 - 33 \times {2}^{x} + 8 \leqslant 0 \\ {t}^{2} \times 4 - 33t + 8 \leqslant 0 \\ t∈[ \frac{1}{4} ;8] \\ {2}^{x} ∈[ \frac{1}{4} ;8 ] \\ {2}^{x} \geqslant \frac{1}{4} \\ {2}^{x} 8 \\ x \geqslant - 2 \\ x \leqslant 3 \\ x∈[ - 2;3 ]$