решить уравнение 35х + 30у = 320

Question

Математика: решить уравнение 35х + 30у = 320

ArtSvet · Accepted Answer

Задача на составление системы уравнений.

Первое уравнение можно составить исходя из условия того, что в одном шкафу было в 4 раза меньше книг, чем во втором.

Кол-во книг в первом шкафу -x.

Кол-во книг во втором шкафу -y.

Получим: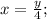
$x=\frac{y}{4};\\$

Второе уравнение системы получим из дальнейшего условия задачи:
Если в первый шкаф (x) положили 17 книг, а из второго (y) взяли 25, то книг в обоих шкафах стало равное кол-во.

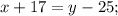
$x+17=y-25;\\$

Получаем систему уравнений, которая решается очень просто: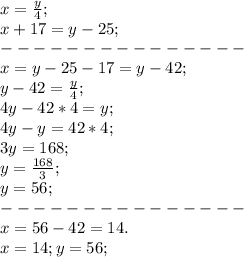
$x=\frac{y}{4};\\ x+17=y-25;\\ ---------------\\ x=y-25-17=y-42;\\ y-42=\frac{y}{4};\\ 4y-42*4=y;\\ 4y-y=42*4;\\ 3y=168;\\ y=\frac{168}{3};\\ y=56;\\ ---------------\\ x=56-42=14.\\ x=14;y=56;\\$

Получили, что в первом шкафу 14 книг, во втором шкафу 56 книг.

ответ: первый шкаф: 14 книг, второй шкаф: 56 книг.

MOGZ ответил