щоб знайти множник потрібно добуток поділити на відомий множник
x=1:8
x=0,125 або 1/8
![y = \sqrt[3]{x^2} e^{ -\frac{x}{3} }](/tpl/images/0479/1434/a5a92.png) ;
;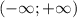 ;
;![y(-x) = \sqrt[3]{ (-x)^2 } e^{ -\frac{-x}{3} } = \sqrt[3]{ x^2 } e^{ \frac{x}{3} }](/tpl/images/0479/1434/a8cb6.png) ;
;![y(-x)/y(x) = \frac{ \sqrt[3]{ x^2 } \exp{ \frac{x}{3} } }{ \sqrt[3]{ x^2 } \exp{ ( -\frac{x}{3} ) } } = \frac{ \exp{ \frac{x}{3} } }{ \exp{ -\frac{x}{3} } } = \exp{ \frac{x}{3} } \exp{ \frac{x}{3} } = \exp{ \frac{2x}{3} }](/tpl/images/0479/1434/2b8d3.png) ≠ ± 1 при любых аргументах ;
≠ ± 1 при любых аргументах ;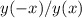 ≠ ± 1 ;
≠ ± 1 ;![y'(x) = ( \sqrt[3]{x^2} e^{ -\frac{x}{3} } )' = ( x^\frac{2}{3} e^{ -\frac{x}{3} } )' = \frac{2}{3} x^{ -\frac{1}{3} } e^{ -\frac{x}{3} } + x^\frac{2}{3} ( -\frac{1}{3} ) e^{ -\frac{x}{3} } =](/tpl/images/0479/1434/77b4d.png)
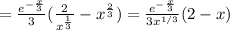 ;
;![y'(x) = \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( 2 - x )](/tpl/images/0479/1434/4a626.png) ;
;![\lim_{x \to -0} y(x) = \lim_{x \to -0} \sqrt[3]{x^2} e^{ \frac{x}{3} } = \sqrt[3]{ (-0)^2 } e^{ -\frac{-0}{3} } = \sqrt[3]{0} e^{0} = 0*1 = 0](/tpl/images/0479/1434/9239a.png) ;
;![\lim_{x \to +0} y(x) = \lim_{x \to +0} \sqrt[3]{x^2} e^{ \frac{x}{3} } = \sqrt[3]{ (+0)^2 } e^{ -\frac{0}{3} } = \sqrt[3]{0} e^{0} = 0*1 = 0](/tpl/images/0479/1434/7dd77.png) ;
;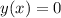 ;
;![\sqrt[3]{x^2} e^{ -\frac{x}{3} } = 0](/tpl/images/0479/1434/13ef8.png) ;
;![\sqrt[3]{x^2} = 0](/tpl/images/0479/1434/9246d.png) , т.е. при x = 0 ;
, т.е. при x = 0 ;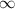 :
:![\lim_{x \to -\infty} y(x) = \lim_{x \to -\infty} \sqrt[3]{x^2} e^{ -\frac{x}{3} } = \lim_{x \to -\infty} e^{ \ln{ \sqrt[3]{x^2} } } e^{ -\frac{x}{3} } =](/tpl/images/0479/1434/2d670.png)
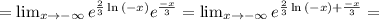
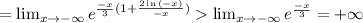 ;
;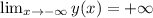 ;
;![\lim_{x \to +\infty} y(x) = \lim_{x \to +\infty} \sqrt[3]{x^2} e^{ -\frac{x}{3} } = \lim_{x \to +\infty} e^{ \ln{ \sqrt[3]{x^2} } } e^{ -\frac{x}{3} } =](/tpl/images/0479/1434/a7ec7.png)
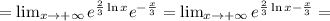
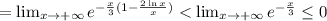 ;
;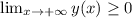 , то:
, то: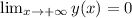 ;
;![\lim_{x \to -\infty} y'(x) = \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( 2 - x ) < \lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( - x )](/tpl/images/0479/1434/440e7.png) ;
;![\lim_{x \to -\infty} \frac{ e^{ -\frac{x}{3} } }{ 3 \sqrt[3]{x} } ( - x ) = \lim_{x \to -\infty} ( -\frac{1}{3} \sqrt[3]{x^2} e^{ -\frac{x}{3} } ) = -\infty](/tpl/images/0479/1434/e2ca5.png) – по доказанному в пределе самой функции .
– по доказанному в пределе самой функции .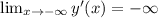 ;
;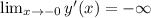 ,
,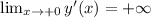 , поскольку:
, поскольку:![\lim_{x \to -0} y'(x) = \lim_{x \to -0} \frac{ e^{ -\frac{-0}{3} } }{ 3 \sqrt[3]{-0} } ( 2 - (-0) ) = -\infty](/tpl/images/0479/1434/18616.png) и:
и:![\lim_{x \to +0} y'(x) = \lim_{x \to +0} \frac{ e^{ -\frac{+0}{3} } }{ 3 \sqrt[3]{+0} } ( 2 - (+0) ) = +\infty](/tpl/images/0479/1434/cef3a.png) ;
;

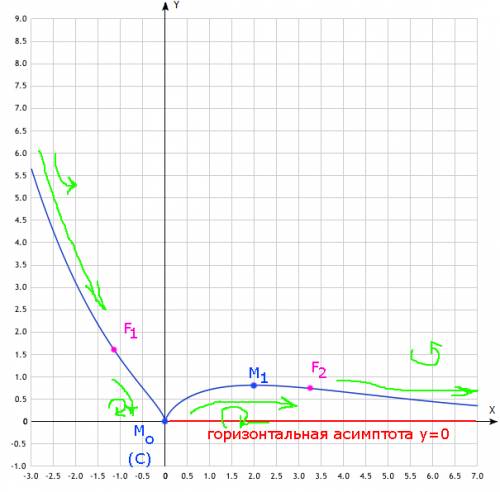
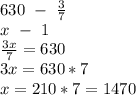
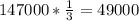

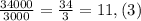
Відповідь:
x=0.225
Покрокове пояснення:
8x=1.8
x=1.8:8
x=0.225