
Исследовать функцию и построить график 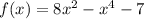
1) Область определения функции. Функция определена на всей числовой оси, то есть 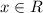
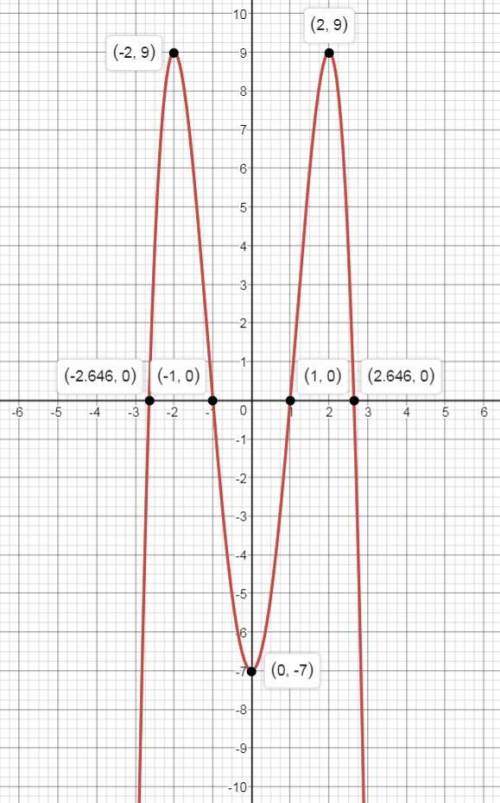
2) Точки пересечения графика функции с осью OY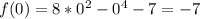 точка пересечение (0; -7)
точка пересечение (0; -7)
Тоски пересечения с осью ОХ, т.е. у=0, тогда
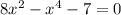
Пусть x² = t, тогда
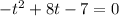
Корни квадратного уравнения t=1 и t=7
Сделаем обратную замену
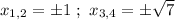
Получили еще четыре точки
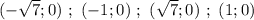
3) Исследуем функции на четность
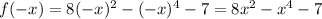
Так как 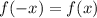 , то функция является четной
, то функция является четной
4) Функция не имеет точек разрыва, поэтому график не имеет вертикальных асимптот.
Найдем наклонные асимптоты  , где
, где
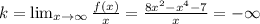
Наклонных асимптот тоже нет.
5) Найдем экстремумы функции. Для это найдем производную y' и приравняем ее к нулю y' = 0
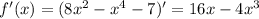
Тогда
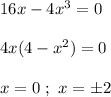
Получились три критические точки.
Эти точки разбивают область определения на четыре интервала. Находим знак производной f'(x) в каждом из интервалов
На первом x < -2 , f'(x) > 0 - функция возрастает
На первом -2 < x < 0 , f'(x) < 0 - функция убывает
На первом 0 < x < 2 , f'(x) > 0 - функция возрастает
На первом x > 2 , f'(x) > 0 - функция убывает
Таким образом в при х=-2 и х = 2 - тока максимума,
а при х = 0 - тока минимума.
1.
2.
3.
Снова получили исходный интеграл
Пусть
тогда