x^2 + y^2 = 20; 3x + y = 2. Выразим у из второго уравнения и подставим в первое уравнение.
у = 2 - 3х;
x^2 + (2 - 3х)^2 = 20;
раскрываем скобки по формуле квадрата разности: x^2 + 4 - 12х + 9х^2 - 20 = 0;
подводим подобные слагаемые: 10x^2 - 12х - 16 = 0;
поделим уравнение на 2: 5x^2 - 6х - 8 = 0.
Решаем квадратное уравнение с дискриминанта:
a = 5; b = -6; c = -8;
D = b^2 - 4ac; D = (-6)^2 - 4 * 5 * (-8) = 36 + 160 = 196 (√D = 14);
x = (-b ± √D)/2a;
х1 = (6 + 14)/(2 * 5) = 20/10 = 2.
х2 = (6 - 14)/10 = -8/10 = 0,8.
Так как у = 2 - 3х, то у1 = 2 - 3 * х1 = 2 - 3 * 2 = 2 - 6 = -4;
у2 = 2 - 3 * х2 = 2 - 3 * 0,8 = 2 - 2,4 = -0,4.
ответ: (2; -4) и (0,8; -0,4).
Сложим оба уравнения системы и решим полученное уравнение:
4x2 - xy = 26;
3x2 + xy = 2;
7х2 = 28;
х2 = 4;
х1 = 2; х2 = - 2;
Далее из второго уравнения системы выразим и найдём значение у:
3x2 + xy = 2;
ху = 2 - 3x2;
у = (2 - 3x2)/х;
у1 = (2 - 3 * 4)/2 = - 5;
у2 = (2 - 3 * 4)/( - 2) = 5.
Пошаговое объяснение:
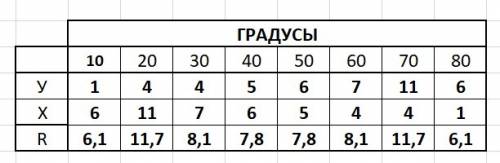
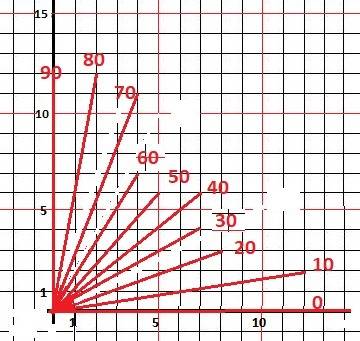
1) Берём транспортир и делаем рисунок до пересечения с узлом сетки - в приложении.
2) Заполняем таблицу с результатами измерений. Узел обозначаем точкой на рисунке и двумя координатами в таблице. Таблица в приложении. А на рисунке они не обозначены, чтобы их было видно.
3) Определить путь - измерить расстояние линейкой между этими точками и началом координат. Можно и вычислить по теореме Пифагора гипотенузу: c = √(x²+y²).
4) Сравнить результаты - отношения Х и У - обратные -
1/6 и 6/1, 4/11 и 11/4, а длины отрезков - равные.
5) Построить силой Разума угол примерно 30° - запросто - семь направо четыре вверх.
Дополнительно.
45° = 1/1.
у першій 52
у другій 13
Пошаговое объяснение: