Вычисляем определитель матрицы 3×3:
∆ =
5 3 3
2 6 -3
8 -3 2
= 5·6·2 + 3·(-3)·8 + 3·2·(-3) - 3·6·8 - 5·(-3)·(-3) - 3·2·2 = 60 - 72 - 18 - 144 - 45 - 12 = -231.
Находим определители:
∆1 =
48 3 3
18 6 -3
21 -3 2
= 48·6·2 + 3·(-3)·21 + 3·18·(-3) - 3·6·21 - 48·(-3)·(-3) - 3·18·2 = 576 - 189 - 162 -
- 378 - 432 - 108 = -693.
∆2 =
5 48 3
2 18 -3
8 21 2
= 5·18·2 + 48·(-3)·8 + 3·2·21 - 3·18·8 - 5·(-3)·21 - 48·2·2 = 180 - 1152 + 126 - 432 + 315 - 192 = -1155.
∆3 =
5 3 48
2 6 18
8 -3 21
= 5·6·21 + 3·18·8 + 48·2·(-3) - 48·6·8 - 5·18·(-3) - 3·2·21 = 630 + 432 - 288 - 2304 + 270 - 126 = -1386.
x = ∆1 / ∆ = -693 / -231 = 3.
y = ∆2 / ∆ = -1155 / -231 = 5.
z = ∆3 / ∆ = -1386 / -231 = 6.
ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
![\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/e1322.png)
Приведем к ступенчатому виду. Применяем операцию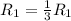 
к 
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/6eddc.png)
Применяем операцию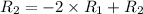 
к 
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию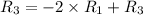 
к 
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/0d2b8.png)
Применяем операцию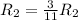 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/8a8f7.png)
Применяем операцию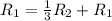 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/c212b.png)
Применяем операцию 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]](/tpl/images/1055/0577/960ac.png)
Применяем операцию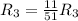 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/ffa18.png)
Применяем операцию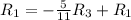 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/a5101.png)
Применяем операцию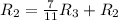 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]](/tpl/images/1055/0577/927aa.png)
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
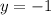
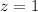
Решением является множество упорядоченных пар, которые удовлетворяют системе.
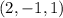
1) ответ: дочери 4 года
2) ответ: 4 овцы и 15 кур
3) ответ: 8м меньшая, 280м большая
4) ответ : на первой полке стояло 50 книг, а на второй 22
5) ответ: расстояние велосипедиста 20 * 2 = 40 км
расстояние мотоциклиста 70*2 = 140 км
Пошаговое объяснение:
1) Пусть возраст дочери х, тогда возраст отца 8х, еще возраст отца = х + 28
значит
х + 28 = 8х
7х = 28
х = 28/7
х=4
2) Пусть х овцы, всего 19 голов, значит и 19 животных, тогда кур 19 - х
у курицы 2 ноги, значит ног у кур (19-х)*2
у овцы 4 ноги, значит ног у овец х*4
составим уравнение
(19-х)*2 + х*4 = 46
38 - 2х+ 4х = 46
4х-2х=46-38
2х = 8
х = 4 овец
19 - 4 = 15 кур
3) Пусть х м меньшая часть, тогда 35х м большая часть
составим уравнение
х + 35х = 288
36х = 288
х = 8 м меньшая часть
35 * 8 = 280 м большая часть
4) Пусть х количество книг на второй полке
(х +14)*2=72
х+14 = 72/2
х+14 = 36
х=22 на второй полке
72 - 22 = 50 на первой полке
5) Пусть скорость велосипедиста х, тогда скорость мотоциклиста 50+х
(х + 50 +х ) * 2 = 180 км
2х + 50 = 90
2х = 40
х = 20 км/ч
тогда скорость мотоциклиста 20+50 = 70 км/ч
расстояние велосипедиста 20 * 2 = 40 км
расстояние мотоциклиста 70*2 = 140 км