Первоначально в бригаде было x рабочих, которые работали по y часов в день.
Производительность всей бригады 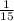 всей работы в день или
всей работы в день или  всей работы в час.
всей работы в час.
Производительность одного рабочего 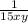 всей работы в час.
всей работы в час.
Если бригадир наймет девять дополнительных рабочих, и при этом в день бригада будет работать на 2 часа меньше, то работа будет выполнена за 12 дней, то есть
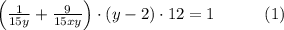
Если бригадир уволит пятерых рабочих из первоначального состава бригады, то, чтобы окончить работу за 20 дней, бригаде придётся трудиться на 2 часа в день больше, то есть
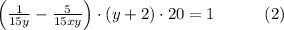
Составим и решим систему уравнений (1) и (2):

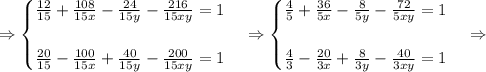
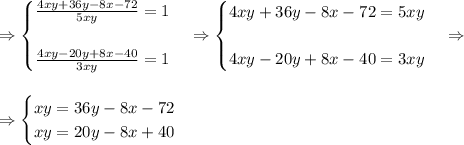
Вычтём из первого уравнения второе:
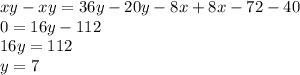
Подставим значение y в любое из двух уравнений систему (например, во второе) и вычислим x:
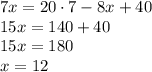
Тогда
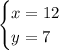
ответ: первоначально в бригаде было 12 рабочих, которые работали по 7 часов в день.
среднее значение = 10 13/19 ≈ 10,68
мода = 10,
медиана = 10
Пошаговое объяснение:
13,14,9,10,10,12,11,8,9,6,10,10,13,15,10,8,14,10,11
среднее значение = сумма усредняемого признака / число единиц совокупности==(13+14+9+10+10+
+12+11+8+9+6+
+10+10+13+15+10+
+8+14+10+11) / 19 =
= 203 / 19 = 10 13/19 ≈ 10,68
мода - значение признака, которое наиболее часто встречается в совокупности (мод может быть несколько)для упрощения подсчёта упорядочим ряд по возрастанию значения исследуемого признака:
6, 8, 8, 9, 9, 10, 10, 10, 10, 10, 10, 11, 11, 12, 13, 13, 14, 14, 15
итого:
6 - 1 шт,
8 - 2 шт,
9 - 2 шт,
10 - 6 шт, - наиболее часто встречаемый признак
11 - 2 шт,
12 - 1 шт,
13 - 2 шт,
14 - 2 шт,
15 - 1 шт
следовательно, мода = 10
медиана - значение признака, которое находится в середине вариационного ранжированного рядарассмотрим ещё раз наш упорядоченный по возрастанию ряд:
6, 8, 8, 9, 9, 10, 10, 10, 10, 10 (значение в середине ряда), 10, 11, 11, 12, 13, 13, 14, 14, 15