Математика: впр идёт найдите значение выражения 2,4:1, 2*2, 5

впр идёт найдите значение выражения 2,4:1, 2*2, 5

👇

Увидеть ответ

Ответ:

AKA1111173

12.08.2020

4,5(86 оценок)

Открыть все ответы

Ответ:

Маслинка174

12.08.2020

Пошаговое объяснение:

рисунок во вложении

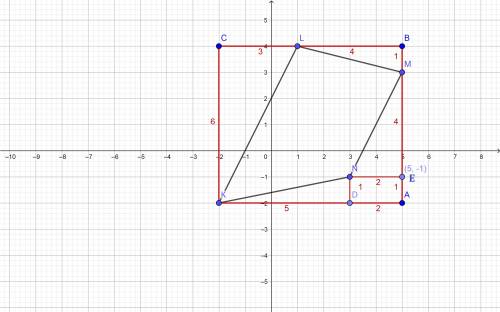
Построим прямоугольник KCBA

проходящий через вершины K,L,M четырехугольника KLMN

Найдем площадь получившегося прямоугольника

S прям KCBA=a*b

S=6*7=42 cм²

Теперь найдем площади прямоугольных треугольников

KCL, LBM. MEN ,KDN и прямоугольника DNEA

Формула площади прямоугольного треугольника

S=1/2 a*b, где a и b катеты

$S_{KCL}=\frac{1}{2} *KC*CL=(6*3)/2=9~cm^{2} \\ \\S_{LBM}=\frac{1}{2}*LB*BM=(4*1)/2=2~cm^{2} \\ \\ S_{MEN}=\frac{1}{2}*ME*EN=(4*2)/2=4~cm^{2} \\ \\S_{NDK}=\frac{1}{2}*KD*DN=(5*1)/2=2,5~cm^{2} \\ \\ S_{DNEA}=2*1=2~cm^{2}$

Теперь вычтем все площади треугольников и прямоугольника DNEA из площади прямоугольника KCBA и получим площадь четырехугольника KLMN

S=42-9-2-4-2,5-2=22,5 см²

ответ: площадь четырехугольника KLMN составляет 22,5 см²

P.S. Я надеюсь, что вы все это уже изучали

Вычислите площадь четырёхугольника, вершины которого находятсяа точках к(-2; - 2), l(1; 4), m(5; 3),

4,8(60 оценок)

Ответ:

Алёна0Чан

12.08.2020

Для описания распределения вероятностей непрерывной случайной величины используется дифференциальная функция распределения.
Дифференциальная функция распределения (ДФР) (или плотность вероятности) – это первая производная от интегральной функции.

Интегральная функция распределения является первообразной для дифференциальной функции распределения. Тогда

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:

Геометрический смысл ДФР состоит в следующем: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью x, кривой распределения f(x) и прямыми x = a и x = b (рис. 4).

Рис. 4 График дифференциальной функции распределения принято называть кривой распределения.
Свойства дифференциальной функции распределения:
1. Дифференциальная функция распределения неотрицательна, т. е.
2. Если все возможные значения случайной величины принадлежат интервалу (a, b), то

Дифференциальную функцию распределения часто называют законом распределения вероятностей непрерывных случайных величин.
При решении прикладных задач сталкиваются с различными законами распределения вероятностей непрерывных случайных величин. Часто встречаются законы равномерного и нормального распределения.
1.5. Равномерное распределение непрерывной случайной величиныЗакон равномерного распределения вероятностей непрерывной случайной величины используется при имитационном моделировании сложных систем на ЭВМ как первоначальная основа для получения всех необходимых статистических моделей. При этом, если специально не оговорен закон распределения случайных чисел, то имеют ввиду равномерное распределение.
Распределение вероятностей называют равномерным, если на интервале (a,b), которому принадлежат все возможные значения случайной величины, дифференциальная функция распределения имеет постоянное значение, т. е. f(x) = C.
Так как

то

Отсюда закон равномерного распределения аналитически можно записать так:

График дифференциальной функции равномерного распределения вероятностей представлен на рис.5

Рис. 5 График дифференциальной функции равномерного распределения вероятностей.
Интегральную функцию равномерного распределения аналитически можно записать так:

График интегральной функции равномерного распределения вероятностей представлен на рис. 6

Рис. 6 График интеграль

4,5(66 оценок)

Это интересно:

Кулинария-и-гостеприимство

16.11.2022

Как собрать идеальный пляжный обед?...

Хобби-и-рукоделие

06.04.2022

Как разгладить мятую бумагу: простые методы и советы...

Образование-и-коммуникации

06.10.2021

Как решать кубические уравнения: подробное руководство...

27.06.2021