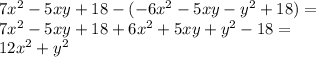. Есть константа(число) и переменные, содержащие степень. А например
. Есть константа(число) и переменные, содержащие степень. А например 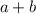 одночленом уже не будет.
одночленом уже не будет.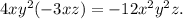 .
. 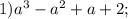
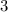

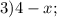
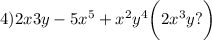
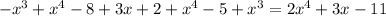
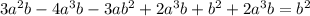
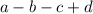 в виде:
в виде: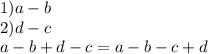
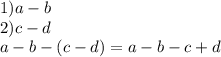
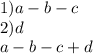

 и
и 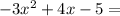 .
.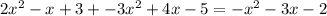
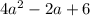 и
и 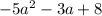 .
.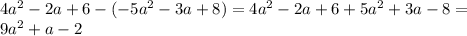
 и
и 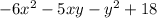 .
.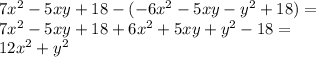
 . Есть константа(число) и переменные, содержащие степень. А например
. Есть константа(число) и переменные, содержащие степень. А например 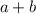 одночленом уже не будет.
одночленом уже не будет.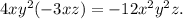 .
. 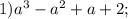
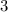

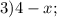
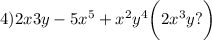
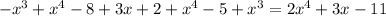
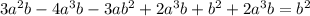
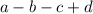 в виде:
в виде: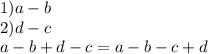
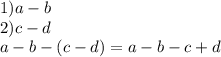
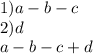

 и
и 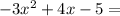 .
.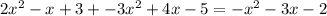
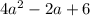 и
и 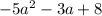 .
.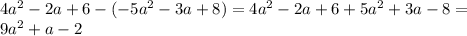
 и
и 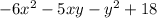 .
.