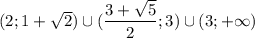
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть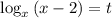 
. Тогда 
:
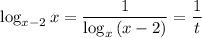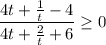. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 
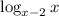равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
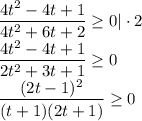
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
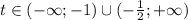
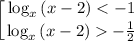
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
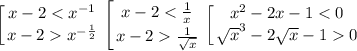
Первое неравенство имеет решение (с учётом ОДЗ)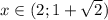 
Второе неравенство раскладывается на множители:
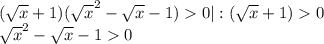
Нули получившегося неравенства: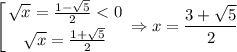 
C учётом ОДЗ получаем, что в данном случае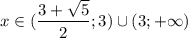 
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
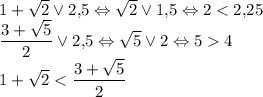
Тогда промежутки не пересекаются, итоговый ответ: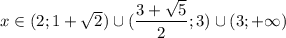 
-1
Пошаговое объяснение:
p(a) = a(10 - a) / (a - 5)
это означает, что если а = 0
p(0) = 0 (10 - 0) / (0 - 5) = 0
или если а = 1
p(1) = 1 (10 - 1) / (1 - 5) = -9/4 = -2.55
теперь, скажем, что а = 10 - а
p(10 - a) = (10 - a) (10 - (10 - a)) / (10 - a - 5) = (10 - a) * a / (5 - a) = a * (10 - a) / (5 - a)
посмотрим, что означает p(0) / p(1) = 0 / -2.55
по аналогии p(a) / p(10 - a) = (a(10 - a) / (a - 5)) / ( a * (10 - a) / (5 - a)) =
(a * (10 - a) * (5 - a)) / ((a - 5) * (10 - a) * a) = (5 - a) / (a - 5) = -1
Діамантовий берег» характеристика
На природі відбуваються серйозні й кумедні події з учнями молодого педагога Григорія Савича, героя повісті «Діамантовий берег». Учитель і школярі Пилип, Хома, Тимофій, Куприк, Женька, Оля, Люся постійно взаємодіють, вчать один одного і разом краще пізнають багато нового за час їхньої літньої експедиції від Полтавщини до одного з північних районів України.
Письменник показує прагнення дітей до пізнання нового:
Пилип своїм «археологічним» ножем робить розкопки пагорбів і допомагає Люсі викопувати рослини для гербарію.
Куприк мріє служити на флоті, марить морем, похід сприймає як екзамен на готовність до випробувань.
Автор підкреслює інтерес дітей до пригод і через опис їхніх читацьких смаків: «У Олі було пів-шафи томів Майна Ріда, Юрія Смолича, Джека Лондона, Миколи Трублаїні. Портрет Миколи Трублаїні висів у Олі над ліжком»
Вибір пригодницького сюжету для повісті про школярів зумовлений педагогічним досвідом автора.
Гумористичному забарвленню повісті “Діамантовий берег” сприяє розповідь про двох повноправних членів експедиції – собаки Білана й вислюка Явтуха, які не лише розмовляють подумки, але й з власної ініціативи охороняють знайдені скарби. Посилює гумористичне сприйняття “внутрішній монолог” бліх, який передає їхнє обурення тим, що Білан посмів полізти у воду й таким чином потурбував їх. Такий прийом, наближаючи дитячий твір до казки, надає йому особливої теплоти
Повість «Діамантовий берег» насичена педагогічними роздумами молодого вчителя, який вимагає дисципліни в поході, але й дає дітям можливість самовияву, самоствердження. Автор не пропонує готових рецептів виховання, не ідеалізує молодого вчителя. Усі персонажі показані в стані пошуків свого «я» і в діалогічних зв’язках типу «дитина-дитина», «дитина-дитячий колектив», «дитина-батьки й родичі», «учитель-учень», «учитель-дитячий колектив», «учитель-батьки», «учитель-колеги».
Ось приклад роздумів Григорія Савича над поведінкою Олі, яка зуміла розв’язати на одному уроці математики задачу Лева Толстого, а наступного дня отримала двійку, бо не змогла відповісти на якесь буденне запитання: «Що може вирости з такої людини… Годилося б завести щоденник і в тому щоденнику записувати, яка вона тепер, що з неї стане через десять, двадцять років…Еге ж…Дуже цікаво було б побачити її дорослою. Та і всіх інших…».
Будемо вдячні всім, хто зможе розширити аналіз твору “Діамантовий берег” (додати тему, ідею, сюжет, композицію, проблематику та ін.)
Джерело: https://dovidka.biz.ua/diamantoviy-bereg-analiz