816
Пошаговое объяснение:
100×8=800
2×8=16
800+16=816
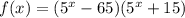
Уравнение касательной имеет вид:
,
где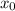 
— абсцисса точки графика функции 
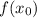, к которому проведена касательная 
.
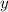Так как график касательной имеет вид график прямой линейной функции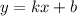 
, а по условию она должна быть горизонтальной, значит, это частый случай линейной функции —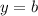 
Таким образом, касательная будет горизонтальной, если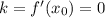 
Найдем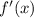 
:
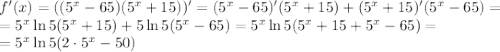
Найдем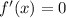 
:
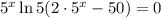
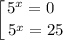
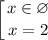
Следовательно,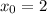 
— абсцисса точки графика функции 
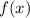, к которому проведена касательная .
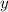Найдем значение :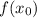
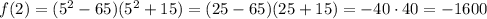
Таким образом,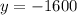 
— уравнение горизонтальной касательной к графику функции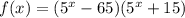
ответ: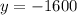
Каждая сторона треугольника меньше суммы двух других сторон. ( Доказательство можете посмотреть в учебнике или найти в сети.)
Следовательно, третья сторона не может быть равна или больше 7+16, т.е. она меньше 23 см.
Но она не может быть меньше разности двух других сторон ( 16-7), так как в противном случае сторона длиной 16 см будет больше суммы длин третьей и первой стороны.
Т.е. третья сторона больше 9 см
Итак, 9 см < 3-я сторона< 23 см
102 умножить на 8 будет 816