Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей с одинаковыми знаменателями.
Правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше
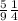
общий 36
первую дробь домножаем на 4,вторую на 9
привели и сравниваем, получается,что
5\9=20\36,1\4=9\36
20\36>9\36 => 5\9>1\4
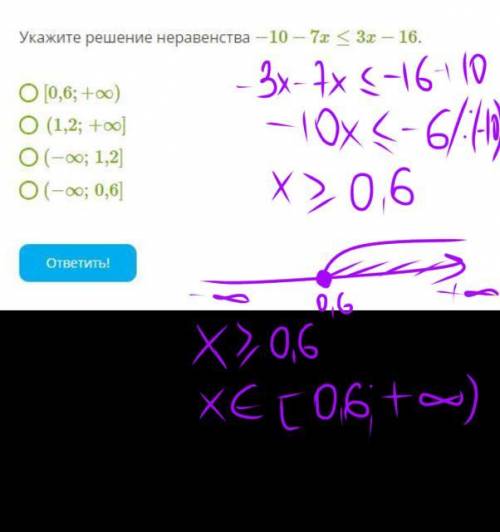
Пошаговое объяснение:
10 * 5^(x - 1) + 5^(x + 1) = 7 - представим показатель второго слагаемого в виде x + 1 = x - 1 + 2;
10 * 5^(x - 1) + 5^(x - 1 + 2) = 7 - второе слагаемое представим в виде произведения степеней 5^(x - 1) * 5^2 на основании свойства степеней: при перемножении степеней с одинаковым основанием показатели степеней складываются, а основание остается прежним a^n * a^n = a^(m + n);
10 * 5^(x - 1) + 5^(x - 1) * 5^2 = 7;
10 * 5^(x - 1) + 25 * 5^(x - 1) = 7;
введем новую переменную 5^(x - 1) = y;
10y + 25y = 7;
35y = 7;
y = 7/35;
y = 1/5.
Возвращаемся к замене.
5^(x - 1) = 1/5;
5^(x - 1) = 5^(- 1) - если основания степеней равны, то , чтобы степени были равны, надо чтобы показатели степеней тоже должны были равны;
x - 1 = - 1;
x = - 1 + 1;
x = 0.
ответ10 * 5^(x - 1) + 5^(x + 1) = 7 - представим показатель второго слагаемого в виде x + 1 = x - 1 + 2;
10 * 5^(x - 1) + 5^(x - 1 + 2) = 7 - второе слагаемое представим в виде произведения степеней 5^(x - 1) * 5^2 на основании свойства степеней: при перемножении степеней с одинаковым основанием показатели степеней складываются, а основание остается прежним a^n * a^n = a^(m + n);
10 * 5^(x - 1) + 5^(x - 1) * 5^2 = 7;
10 * 5^(x - 1) + 25 * 5^(x - 1) = 7;
введем новую переменную 5^(x - 1) = y;
10y + 25y = 7;
35y = 7;
y = 7/35;
y = 1/5.
Возвращаемся к замене.
5^(x - 1) = 1/5;
5^(x - 1) = 5^(- 1) - если основания степеней равны, то , чтобы степени были равны, надо чтобы показатели степеней тоже должны были равны;
x - 1 = - 1;
x = - 1 + 1;
x = 0.
ответ:0