65536
каждой комбинации 0 и 1 в 16 битах представления имеем соответствующее уникальное целое число.
количество таких чисел = 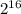 = 65536
= 65536
Пошаговое объяснение:
1) коротко и ясно
пропуская всякие изголяния:
каждой комбинации 0 и 1 в 16 битах представления имеем соответствующее уникальное целое число.
количество таких чисел = 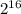 = 65536
= 65536
2) детально
c изголяниями (видимо то, что хочет во
для положительных чисел будем иметь: 0 .. 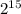 - 1; к-во =
- 1; к-во = 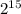
для отрицательных чилел будем иметь: -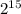 .. -1; к-во =
.. -1; к-во = 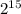
всех чисел будет: к-во положитедьных + к-во отрицательных =
= 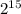 +
+ 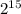 =
= 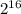
в купе будет все те же 65536
как ньюанс: модуль максимального отр. числа больше модуля макс. пол. числа. На 1.
как то так
"Опасные" точки сразу видны, это:
1)
2)
Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
Выделяем целую часть в дроби:
Используем свойство 2-го замечательного предела, но добавляем степени:
То есть мы степень не меняли: домножили и разделили.
Посчитаем, что получилось:
Итак:
1)
2)
3)
4)
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).
Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.
Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала
Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).
Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).