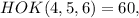
 где
где  – некоторое целое число.
– некоторое целое число.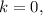 тогда
тогда 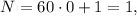 но
но  не делится на
не делится на  а значит не подходит.
а значит не подходит.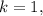 тогда
тогда 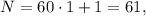 но
но 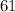 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 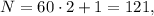 но
но 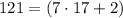 не делится на
не делится на  а значит не подходит.
а значит не подходит.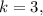 тогда
тогда 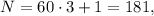 но
но 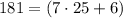 не делится на
не делится на  а значит не подходит.
а значит не подходит.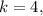 тогда
тогда 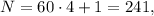 но
но 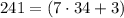 не делится на
не делится на  а значит не подходит.
а значит не подходит. тогда
тогда 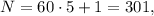 и
и 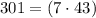 – делится на
– делится на  а значит подходит !
а значит подходит !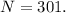
 где
где  – некоторое целое число.
– некоторое целое число.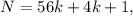 где
где  – некоторое целое число.
– некоторое целое число.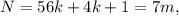 где
где  и
и 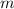 – некоторые целые числа.
– некоторые целые числа.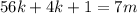 ;
;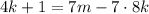 ;
;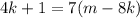 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: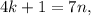 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.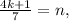 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 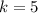 ;
;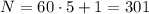 ;
; где
где  – некоторое целое число.
– некоторое целое число.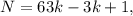 где
где  – некоторое целое число.
– некоторое целое число. где
где  и
и 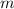 – некоторые целые числа.
– некоторые целые числа.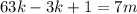 ;
;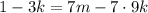 ;
;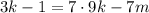 ;
;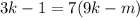 – правая часть здесь кратна семи, а значит и левая кратная семи, т.е.:
– правая часть здесь кратна семи, а значит и левая кратная семи, т.е.: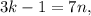 где
где  и
и  – некоторые целые числа.
– некоторые целые числа.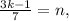 где
где  и
и  – некоторые целые числа.
– некоторые целые числа. а значит:
а значит: где
где 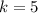 ;
;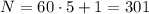 ;
;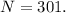
Значит искомое число солдат:
П е р в ы й . п у т ь . р е ш е н и я :
Пусть
Пусть
Пусть
Пусть
Пусть
Пусть
И это минимальное число солдат:
В т о р о й . п у т ь . р е ш е н и я :
Как мы выяснили
Преобразуем
И это число, с другой стороны кратно семи, т.е.
Итак:
что возможно при самом малом
Т р е т и й . п у т ь . р е ш е н и я :
Как мы выяснили
Преобразуем
И это число, с другой стороны кратно семи, т.е.
Итак:
что возможно при самом малом
О т в е т :