
a=-6
Пошаговое объяснение:
(|x|-2)(|x|-4)=2-a
(|x|-2)(|x|-4)-2+a=0
рассмотрим функцию f(x)=(|x|-2)(|x|-4)-2+a
Она непрерывна на всей числовой оси.
f(-x)=(|-x|-2)(|-x|-4)-2+a=(|x|-2)(|x|-4)-2+a=f(x) ⇒ функция четная.
Если четная функция имеет НЕчетное количество корней, то один из них обязательно будет 0.
для уравнения: (|x|-2)(|x|-4)=2-a, при х=0, получаем
(0-2)(0-4)=2-a
-2*(-4)=2-a
8=2-a
a=2-8
a=-6 - при таком значении a уравнение имеет нечетное число различных корней.
Проверим, будет ли их ровно 3:
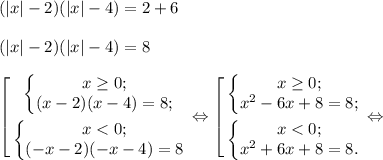
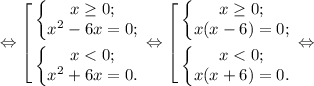
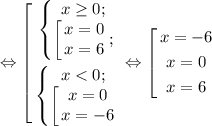
Действительно, при a=-6 получилось 3 корня!
ответ: a=-6
Округляем если следующая 5,6,7,8,9 то +1 к предыдущему; если 0,1,2,3,4 то ничего не добавляем.
Абсолютная погрешность приближенного числа это модуль разности данного числа и его приближенного значения.
1) 0.8
0,8=~~ 1 округлённое до единиц
|1-0,8|=0,2 абсолютная погрешность
2)7.6
7,6=~~ 8 округлённое до единиц
|8-7,6|=0,4 абсолютная погрешность
3)19.3
19,3=~~19 округлённое до единиц
|19-19,3|=|-0,3|=0,3 абсолютная погрешность
4)563.58
563,58=~~564 округлённое до единиц
|564-563,58|= 0,42 абсолютная погрешность