1-й вел. за 1 час; 2-й вел. за 1/2 часа; встреча через ? мин Решение. 1 с п о с о б. V = S / t если второй велосипедист тратит на одинаковый путь в два раза меньше времени, то его скорость в два раза больше, чем у первого. S = V * t если время одинаково (выехали одновременно, и встретились), то второй до встречи проходит путь в два раза больше. 1 часть пути проходит первый велосипедист; 2 части пути проходит второй велосипедист. 1 + 2 = 3 (части) весь путь. Время до встречи: 60 мин * 1/3 =20 мин - потребуется первому велосипедисту на 1/3 пути до встречи; ответ: в) 20 мин Проверка: 30 мин *2/3 = 20 мин. Встретятся! 2 с п о с о б. 1 час = 60 мин; 1/2 часа= 30 мин; S = V/t S весь путь; S/60 скорость первого; S/30 скорость второго; (S/60) + (S/30) = 3S/60 = S/20 общая скорость (V) t = S/V = S/(S/20) = 20 (мин) время встречи ответ: в) 20 мин
1-й вел. за 1 час; 2-й вел. за 1/2 часа; встреча через ? мин Решение. 1 с п о с о б. V = S / t если второй велосипедист тратит на одинаковый путь в два раза меньше времени, то его скорость в два раза больше, чем у первого. S = V * t если время одинаково (выехали одновременно, и встретились), то второй до встречи проходит путь в два раза больше. 1 часть пути проходит первый велосипедист; 2 части пути проходит второй велосипедист. 1 + 2 = 3 (части) весь путь. Время до встречи: 60 мин * 1/3 =20 мин - потребуется первому велосипедисту на 1/3 пути до встречи; ответ: в) 20 мин Проверка: 30 мин *2/3 = 20 мин. Встретятся! 2 с п о с о б. 1 час = 60 мин; 1/2 часа= 30 мин; S = V/t S весь путь; S/60 скорость первого; S/30 скорость второго; (S/60) + (S/30) = 3S/60 = S/20 общая скорость (V) t = S/V = S/(S/20) = 20 (мин) время встречи ответ: в) 20 мин
y = 1,7
x = -0,8
Пошаговое объяснение:
{21x+y=-15,1
{y=0,9-x
21x + y = -15,1
21x + 0,9 - x = -15,1
20x = -15,1 -0,9
20x = -16
x =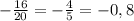
y = 0,9 - x = 0,9 - (-0,8) = 0,9 + 0,8 = 1,7