1) 0,3(5х -7) = 3(0,2х +3,2)
1,5х-2,1=0,6х+9,6
1,5х-0,6=9,6+2,1
0,9х=11,7
х=13
2) 3х + 5 = 8х -15
3х-8х=-15-5
-5х=-20
х=4
3) 4(3 - х) - 11 = 7(2х -5)
12-4х-11=14х-35
1-4х=14х-35
-4х-14х=-35-1
-18х=-36
х=2
4) 0,8х + 1,4 = 1,4х - 2,6
0,8х-1,4х=-2,6-1,4
-0,6х=-4
х=6,6
1. х-1 сторона
3х-вторая
х+23-третья
Составим уравнение:
х+3х+х+23=108
5х+23=108
5х=85
х=17 дм 1 сторона
17*3=51 дм вторая сторона
17+23=40 дм третья сторона
2.х книг было в 1 шкафу
4х книг было во 2 шкафу
х + 17 книг стало в 1 шкафу
4х - 25 стало во 2 шкафу.
ПО условию известно, что когда в первый шкаф положили 17 книг,а из второго взяли 25,то в обоих шкафах стало поровну.
4х - 25 = х + 17
4х - х = 17 + 25
3х = 42
х = 14
14 книг было в 1 шкафу
4 * 14 = 56 книг было во 2 шкафу
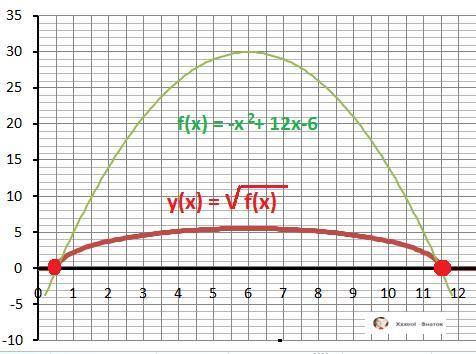
Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).
У25=322:7
У25=46
У=46:25
У=1,84