Длина изогнутой линии 420 см.
Объяснение:
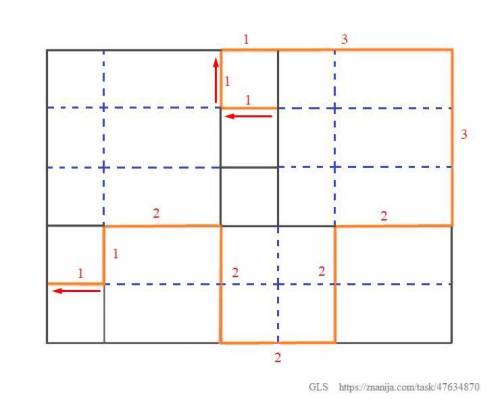
Найти длину отмеченной (оранжевой) линии на рисунке с изображением квадратов. Известно, что сторона меньшего квадрата 20 см.
Квадрат - это четырехугольник, у которого все стороны равны, все углы прямые.
1) Проведем на рисунке вс линии пунктиром, для того, чтобы оценить стороны всех квадратов (смотрим приложение).
2) Теперь мы видим, что
- сторона среднего квадрата равна двум сторонам наименьшего квадрата,
- сторона самого большого квадрата равна трем сторонам наименьшего квадрата.
3) Посчитаем, сколько раз длина стороны наименьшего квадрата входит в длину изогнутой линии.
Расставим количество длин маленького квадрата для каждого звена ломаной.
Посчитаем, сколько таких отрезков получилось.
Считать будем от верхнего малого квадрата по часовой стрелке и завершим подсчет на самом правом малом квадрате.
1 + 1 + 1 + 3 + 3 + 2 + 2 +2 +2 + 2 + 1 + 1 =
= 3 · 1 + 2 · 3 + 5 · 2 + 2 · 1 =
= 3 + 6 + 10 + 2 = 21.
4) Зная, что сторона малого квадрата равна 20 см, вычислим длину всей ломаной.
21 · 20 см = 420 см.
Длина изогнутой линии 420 см.
1996 и 2014
Решение:Очевидно, что числа должны быть четырёхзначные, так как наибольшее трёхзначное число - 999, не удовлетворяет условие задания (999+27<2021)
Пусть наше число будет abcd = 1000a+100b+10c+d.
Так как 1001а должно быть меньше 2021, 1≤а≤2.
1≤a≤2, 0≤b≤9, 0≤c≤9, 0≤d≤9.
Запишем уравнение:
1000а+100b+10c+d+a+b+c+d=2021
1001a+101b+11c+2d = 2021
Начнём рассматривать варианты:
1. а=1
101b+11c+2d=2021-1001
101b+11c+2d=1020
b=911c+2d=1020-101*9
11c+2d=111
c=92d=111-99
2d=12
d=6Соответственно, мы имеем первое число - 1996.
Рассматривать вариант b<9 при а=1 не имеет смысла, так как 11с+2d<212. Поэтому, при а=1 единственный возможный вариант мы нашли.
2. а=2
101b+11c+2d=2021-2002
101b+11c+2d=19
b=011c+2d=19
с=12d=19-11
d=4Имеем второе число - 2014
При а=2 и b>0, 1001а+101b>2021, поэтому при а=2 единственный возможный вариант цифры b - b=0.
При а=2, b=0, с должно быть равно 1, так как:
2002+0+0+2d<2021
2002+0+22+2d>2021
Единственный вариант d при а=2, b=0, с=1 - d=4.
Соответственно, существует только два таких числа - 1996 и 2014.
=148
ВОТ ДОЛЖНО БЫТЬ ПРАВИЛЬНО