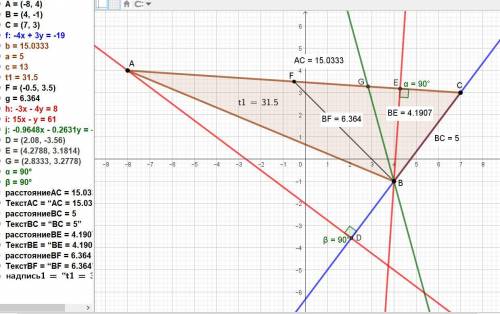
Задані координати вершин трикутника АВС: А(-8;4), В(4;-1), С(7;3).
Знайти:
1) довжину і рівняння сторони ВС.
Вектор ВС = (7-4; 3 –(-1)) = (3; 4).
Модуль (длина) равен √(3² + 4²) = √25 = 5.
Определяем уравнение стороны ВС.
ВС: (x - 4)/3 = (y + 1)/4 каноническое,
4x - 3y - 19 = 0 общее,
y = (4/3)x – (19/3) с угловым коэффициентом.
2) площу трикутника АВС.
Она равна половине модуля векторного произведения векторов ВА и ВС.
Находим ВА = (-8-4; 4 –(-1)) = (-12; 5).
Модуль равен √(-12)² + 5²) = √169 = 13.
Находим векторное произведение ВА и ВС с применением схемы Саррюса.
BAxBC = I j k| I j
-12 5 0| -12 5
3 4 0| 3 4 = 0i + 0j – 48k – 0j – 0i -15k = (0; 0; -63).
S(ABC) = (1/2)√(0² + 0² + (-63)²) = (1/2)*63 = 63/2 = 31,5 кв. ед.
3) рівняння висоти на сторону ВС.
В уравнении высоты AD как перпендикуляра к прямой ВС, общее уравнение которой Ах + Ву + С = 0, коэффициенты А и В меняются на –В и А (из условия, что их скалярное произведение равно 0).
Получаем уравнение AD: 3x + 4y + C = 0. Для определения слагаемого С подставим в уравнение координаты точки А: 3*(-8) + 4*4 + С = 0. Отсюда находим С = 24 – 16 = 8.
Уравнение высоты AD на сторону ВС: 3x + 4y + 8 = 0.
4) кут В в радіанах з точністю до 0,01.
Находим по косинусу угла между векторами ВА и ВС.
Вектор ВА = (-12; 5), модуль 13,
Вектор ВС = (3; 4), модуль 5.
cos B = (-12*3 + 5*4)/(13*5) = -16/65 ≈ -0,24615.
B = arccos (-0,24615)= 1,82 радиан или 104,25 градуса.
5) рівняння бісектриси кута В.
Известно, что биссектриса делит угол пополам. Если на сторонах ВА и ВС треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b.
Для нахождения ортов a и b необходимо знать координаты векторов BA и ВС:
ВА = (-12; 5), модуль равен 13, a = ((-12/13); (5/13)).
ВС (3; 4), модуль равен 5, b = ((3/5); (4/5)).
(a + b) = (((-12/13) + (3/5)); (5/13) + (4/5)) = ((-21/65); (77/65)).
По точке В(4; -1) и направляющему вектору ((-21/65); (77/65)) составляем уравнение биссектрисы BG угла В.
(x – 4)/(-21/65) = (y + 1)/(77/65).
6) довжину і рівняння медіани BF.
Находим координаты точки F как середины стороны АС.
F = (А(-8;4) + С(7;3))/2 = (-0,5; 3,5).
Вектор BF = (F(-0,5; 3,5) - В(4;-1) = (-4,5; 4,5).
Модуль BF = √((-4,5)² +(-4,5)²) = √(20,25 + 20,25) = √40,5 ≈ 6,364.
Уравнение медианы BF составляем по точке В(4;-1) и направляющему вектору BF(-4,5; 4,5).
(x – 4)/(-4,5) = (y + 1)/4,5.
7) довжину висоти ВЕ.
Используем найденное значение площади треугольника АВС и найдём длину стороны АС.
Вектор AC = (C(7; 3) - A((-8);4) = (15; (-1)).
Модуль AC = √((15² +(-1)²) = √(225 + 1) = √226 ≈ 15,0333.
Находим |BE| = 2S(ABC)/|AC| = 2*(63/2)/√226 = 63√226/226 ≈ 4,191.
Крім того він був щей художником, багато його картин збереглися до нашого часу.
Як на мене, то це надзвичайно велика людина, він не дивлячись на життєві труднощі, проблеми та знущання інших людей все одно зумів підняти бойовий та войовничий дух українського народу і змусив людей стати за свою свободу та волю.
Творив в романтизмі та реалізмі. Кожен твір/вірш пронизаний болем, співпереживанням та наздвичайною силою, яка змушувала народ бунтуватися проти влади.
Про Шевченка можна говорити багато. Його вірші перекладалися на різні мови, прославляючи цим Україну.