Округляем до сотых: 2666,25
До сотен: 2700
Пошаговое объяснение:
Это количество должно делиться и на 14, и на 16. Разложим оба этих числа на простые множители:
14=2х7
16=2х2х2х2
Чтобы найти минимальное количество стульев, надо перемножить минимальное количество множителей из приведенных шести, чтобы ответ делился и на 14, и на 16.
Минимальное число, которое делится на 16 - это 16. Среди простых множителей, на которые раскладывается число 16, двойка есть, а вот семерки нет. Но она необходима, иначе число не будет делиться на 14. Зато двоек в числе 16 и так много, целых 4. Значит, без двойки, которая присутствует в равенстве 14=2х7, вполне можно обойтись - ведь число 16 и так делится на 2. А вот больше ни одной двойки выкинуть нельзя - итоговое число тогда не будет делиться на 16.
Значит, одну двойку выкидываем
2х2х2х2х7 = 7х16 = 8х14 = 112.
ответ - в зале 112 стульев. Их можно расставить семью рядами по 16 стульев в каждом ряду, а можно - восемью рядами по 14 стульев.
Рассмотрим какое-нибудь число 
; Пусть 
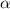- наибольшая степень десятки, которая делит ; Тогда можно представить в виде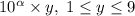 
; Это число имеет 
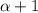цифру. Теперь 
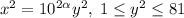; Поэтому число 
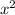имеет в своей записи не больше, чем 
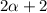цифры, но и не меньше, чем 
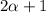цифру.
Если взять первый случай, то пусть первое число ; Тогда второе число - 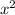, третье - 
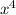; Пусть у 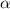цифр, а 
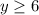; Тогда у первого числа 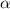цифр, у второго 
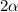, у третьего 
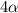. Итого 
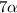цифр. Нас просят, чтоб их было 14. То есть 
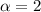. Поэтому, учитывая ограничение на 
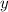, можно взять 
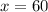; Получим 
;
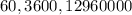Можно было поступить и иначе. Это видно из предыдущего примера. Пусть надо не 14, а 7 цифр. Небольшим перебором можно найти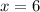 
, а затем заметить, что его можно умножить на 10, тем самым увеличив количество цифр в 2 раза, т.е. до 14
ответ: до сотен 2700, до сотых 2666,25.
Пошаговое объяснение: