1 м 80 см - длина большей из этих частей
Пошаговое объяснение:
Пусть х см длина первой, большей части веревки, тогда вторая часть веревки = х - 30 см, а третья = х - 60 см.
Составим уравнение:
х + (х - 30) + (х - 2 * 30) = 4 м 50 см = 450 см
х + х - 30 + х - 60 = 450
3х = 450 + 90
3х = 540
х = 540 : 3
х = 180 (см) = 1 м 80 см - длина первой, самой большей части веревки
180 см - 30 см = 150 см = 1 м 50 см длина второй части веревки
150 см - 30 см = 120 см = 1 м 20 см длина третьей части веревки
Проверяем:
1 м 80 см + 1 м 50 см + 1 м 20 см = 4 м 50 см
4 м 50 см = 4 м 50 см
1) 14
2) 2 или 3 (см.решение)
3) 
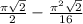
4) 
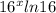
или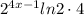 
(см.решение)
5) 
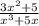
Пошаговое объяснение:
1) 
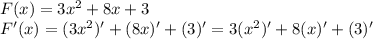
Производная от константы (от тройки), равна нулю.
Производная от 
равна единице.
Производная от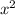 
равна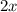 
.
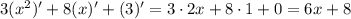
Подставляем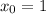 
:
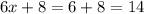
2.1) Если имелось в виду следующее: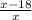 
То здесь надо использовать формулу для производной от частного:
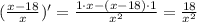
Подставляем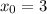 
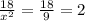
2.2) Если имелось в виду следующее: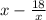 
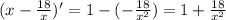
Подставляем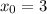
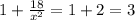
3) 
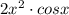
Используем формулу для производной от произведения:
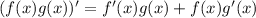
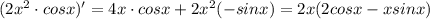
Подставляем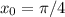 
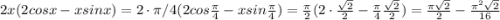
4.1) Если имелось в виду следующее:
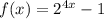
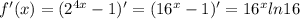
4.2) Если имелось в виду следующее:
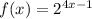
Используется формула для вычисление производной от сложной функции:
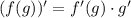
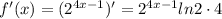
5)
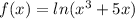
Дифференциируем по правилу для сложной функции:
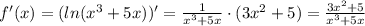
1000-500=500 (на 500рублей больше)