1. Числа, используемые при счёте.
2. Часть отрезка, ограниченная двумя точками.
4. Переместительный (коммутативный) закон сложения: m + n = n + m . Сумма не меняется от перестановки её слагаемых.
Переместительный (коммутативный) закон умножения: m · n = n · m . Произведение не меняется от перестановки его сомножителей.
Сочетательный (ассоциативный) закон сложения: ( m + n ) + k = m + ( n + k ) = m + n + k . Сумма не зависит от группировки её слагаемых.
Сочетательный (ассоциативный) закон умножения: ( m · n ) · k = m · ( n · k ) = m · n · k . Произведение не зависит от группировки его сомножителей.
Распределительный (дистрибутивный) закон умножения относительно сложения: ( m + n ) · k = m · k + n · k .
5. (a+b)*c=a*c+b*c
6. Уравнение – это равенство, содержащее одну или несколько переменных.
7. Вычислить значение перемннной.
11. Приводим к одному знаменателю. У какой дроби числитель больше числителя другой дроби, та и больше.
15. Работаем с числителями.
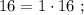
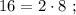
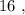т.е.: 
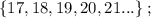
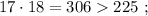
каждое – будет, очевидно, больше чем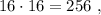 
т.е. больше 
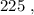а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.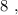
т.е.: 
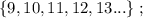
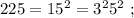
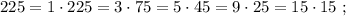
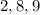и 
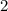и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы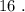 
и никаких натуральных чисел нет. и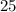 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы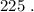 
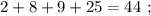
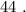
Піску- на 14кг більше ніж цеглини
1)7+14 = 21кг - взяли піску
2) 21:7=3 рази
Відповідь: у 3 рази взяли менше цементу, ніж піску